lodowcowy rowerzysta 371 wyśw. 30-03-2022 18:11

Arkusz 2 zad 1.2


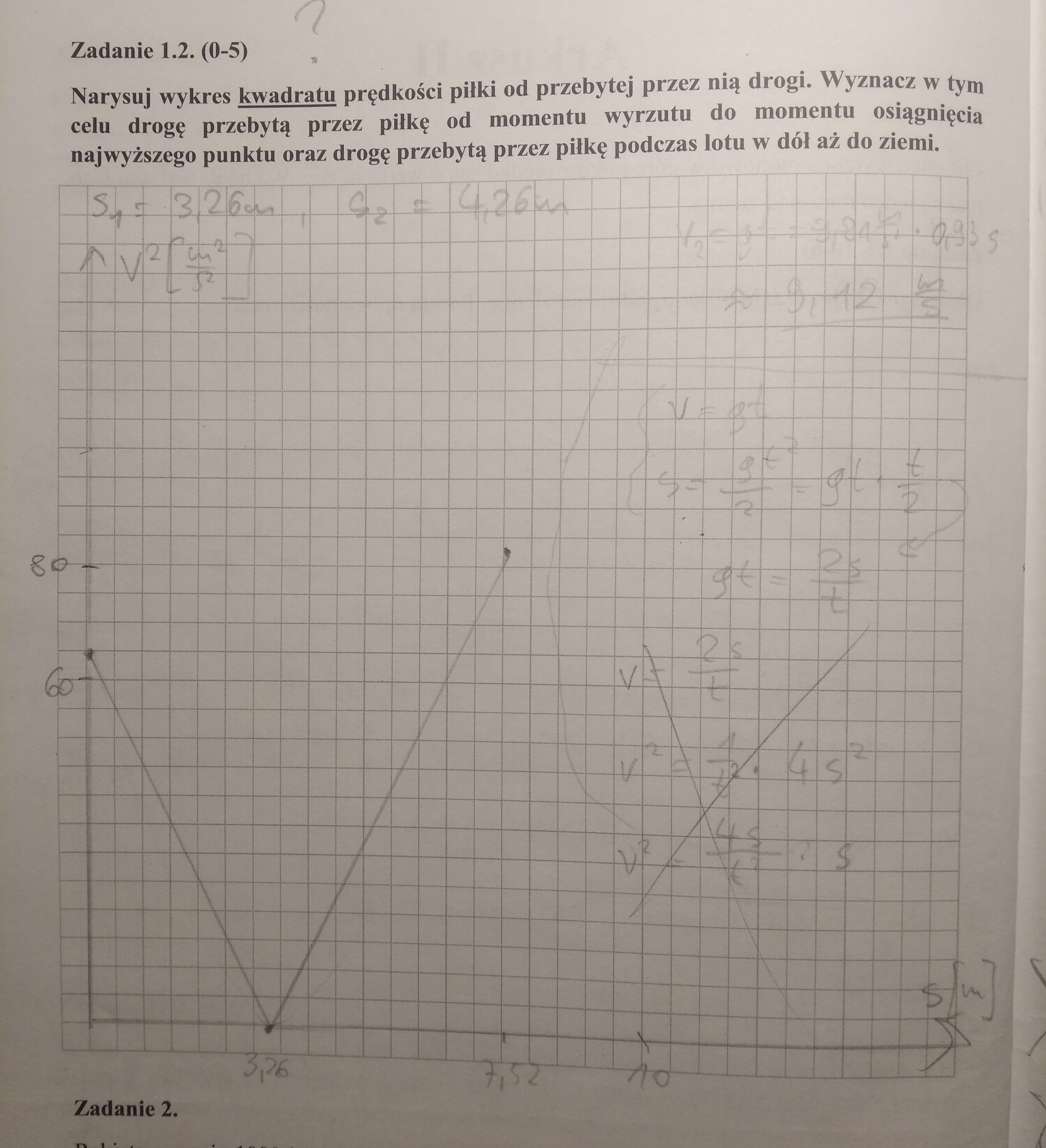
Skąd wiadomo, że to będzie zależność liniowa?
Wykres v^2(s) Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
s.gugula 31-03-2022 10:24

Można to wyznaczyć z równań kinematycznych dla ruchu jednostajnie przyspieszonego (i analogicznie jednostajnie opóźnionego) na prędkość i drogę. Rozpatrzmy np. ruch opóźniony (wyrzut w górę). Ze wzoru na prędkość wyznaczmy czas: $$ v = v_0 - gt  => t = \frac{v_0 - v}{g} $$ i wstawmy go do wzoru na drogę: $$ s = v_0t - \frac{gt^2}{2} $$ Po odpowiednich przekształceniach (wymnożenie wszystkiego i sprowadzenie do wspólnego mianownika) powinniśmy dostać wzór: $$ s = \frac{v_0^2 - v^2}{2g} $$ skąd widzimy, że kwadrat prędkości to: $$ v^2 = v_0^2 - 2sg $$