Arkusz 4 zad 2.4

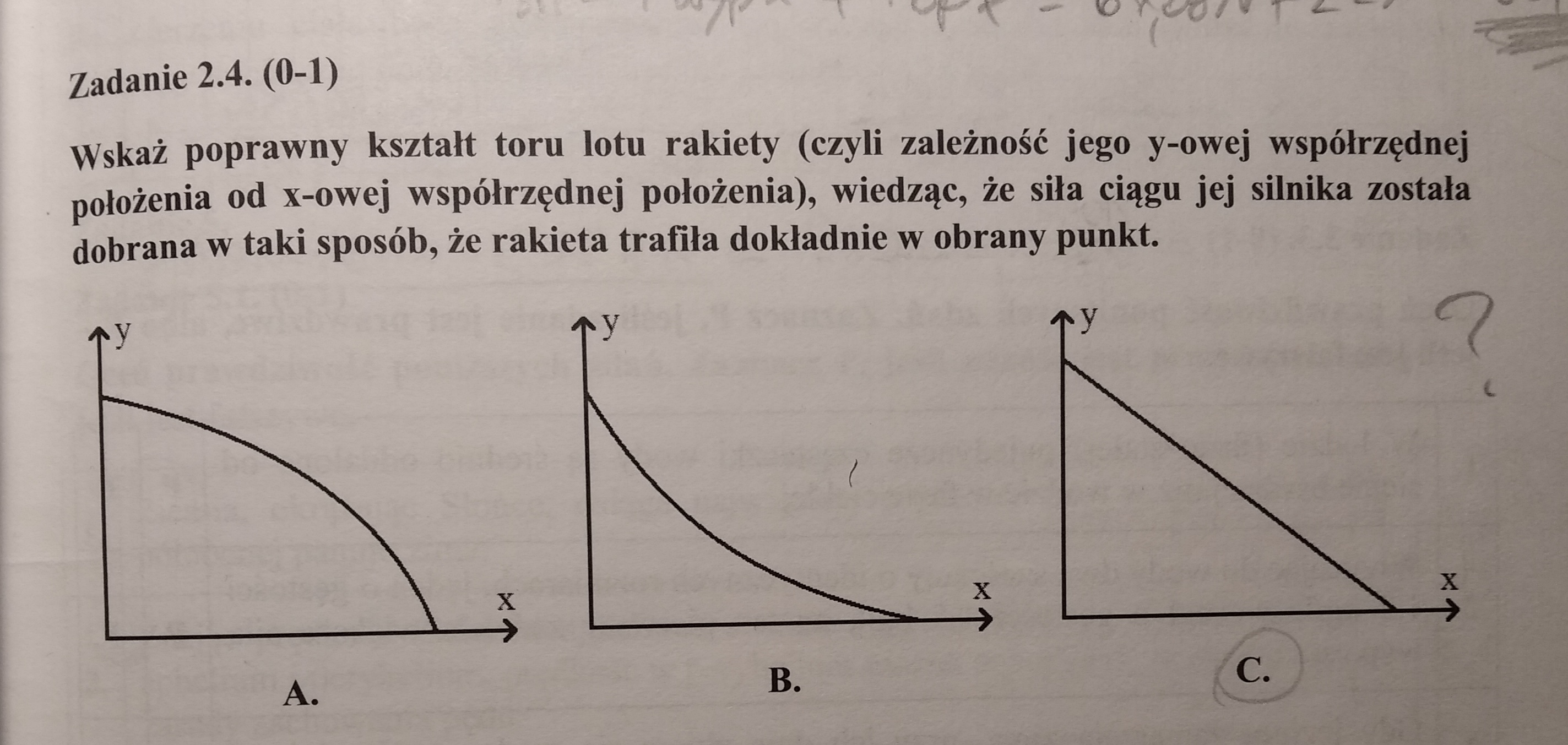
Kształt toru lotu to jak widać zależność y od x, czyli położenia w pionie od położenia w poziomie. Możemy zatem wprost z równań kinematycznych spróbować taką zależność wyciągnąć. W poziomie mamy do czynienia z ruchem jednostajnie przyspieszonym, a zatem przebytą w nim drogę czy też położenie x rakiety możemy opisać następującym wzorem: $$ x = \frac{a_x t^2}{2} $$

W przypadku kierunku pionowego jest to ruch również jednostajnie przyspieszony, przy czym odbywa się on w dół i zaczyna się on od np. jakiejś wysokości h, a zatem położenie w kierunku pionowym możemy zapisać np. tak: $$ y = h - \frac{a_y t^2}{2} $$

I teraz z pierwszego równania możemy np. wyciągnąć t^2 i wrzucić je do drugiego i dostaniemy zależność między y i x: $$ y = h - \frac{a_y}{a_x} x $$ co jak widać jest malejącą funkcją liniową, stąd odpowiedź C.