Arkusz 1 zad 12

Końcowy przedział wychodzi poprawny, lecz dlaczego warunek 5 jest złe rozwiązany? 
Log Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy powinnam dodać jeszcze założenie ze x będzie większe od 1/2?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie, jest po prostu błędnie rozwiązane.
Poprawnie powinno być tak (zakładam, że wcześniej było zrobione założenie dla pierwiastka):
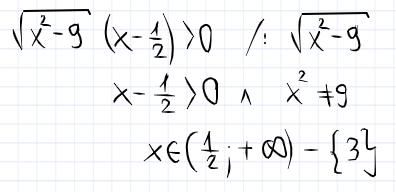
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dlaczego konkretnie ta linijka zaznaczona przez Pana Jarosińskiego w poście z 7 kwietnia jest błędna?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ponieważ Z nierówności nagle przechodzimy do równości
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie rozumiem co w tym złego. Przecież tak zazwyczaj się liczy nierówności. Najpierw obliczenie miejsc zerowych wyrażenia i potem rysunek przebiegu funkcji, z którego odczytujemy przedziały.
Proszę jeszcze o sprawdzenie czy dobrze rozumiem, dlaczego w zamieszczonym przez Pana rozwiązaniu można dzielić przez pierwiastek: mamy iloczyn dwóch liczb jedna z nich (pierwiastek) jest zawsze dodatnia lub równa zero, ale nas interesuje tylko gdy jest dodatnia (ze względu na własności logarytmu), więc całe wyrażenie będzie dodatnie wtedy i tylko wtedy gdy druga liczba będzie dodatnia, więc wystarczy sprawdzić kiedy (x - 1/2) jest dodatnie.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@ lodowcowy rowerzystaTak się rozwiązuje nierówność wielomianową, nie z pierwiastkiem. Powyżej masz moje rozwiązanie, przeanalizuj go i jeśli cokolwiek będzie niejasne to zadaj pytanie do konkretnego przekształcenia :)
Twoje opisane rozumowanie jest poprawne :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ta linijka jest błędna. Zastanów się czemu, a jak sam nie wpadniesz to daj znać i pomogę :)