2018.C.13

---

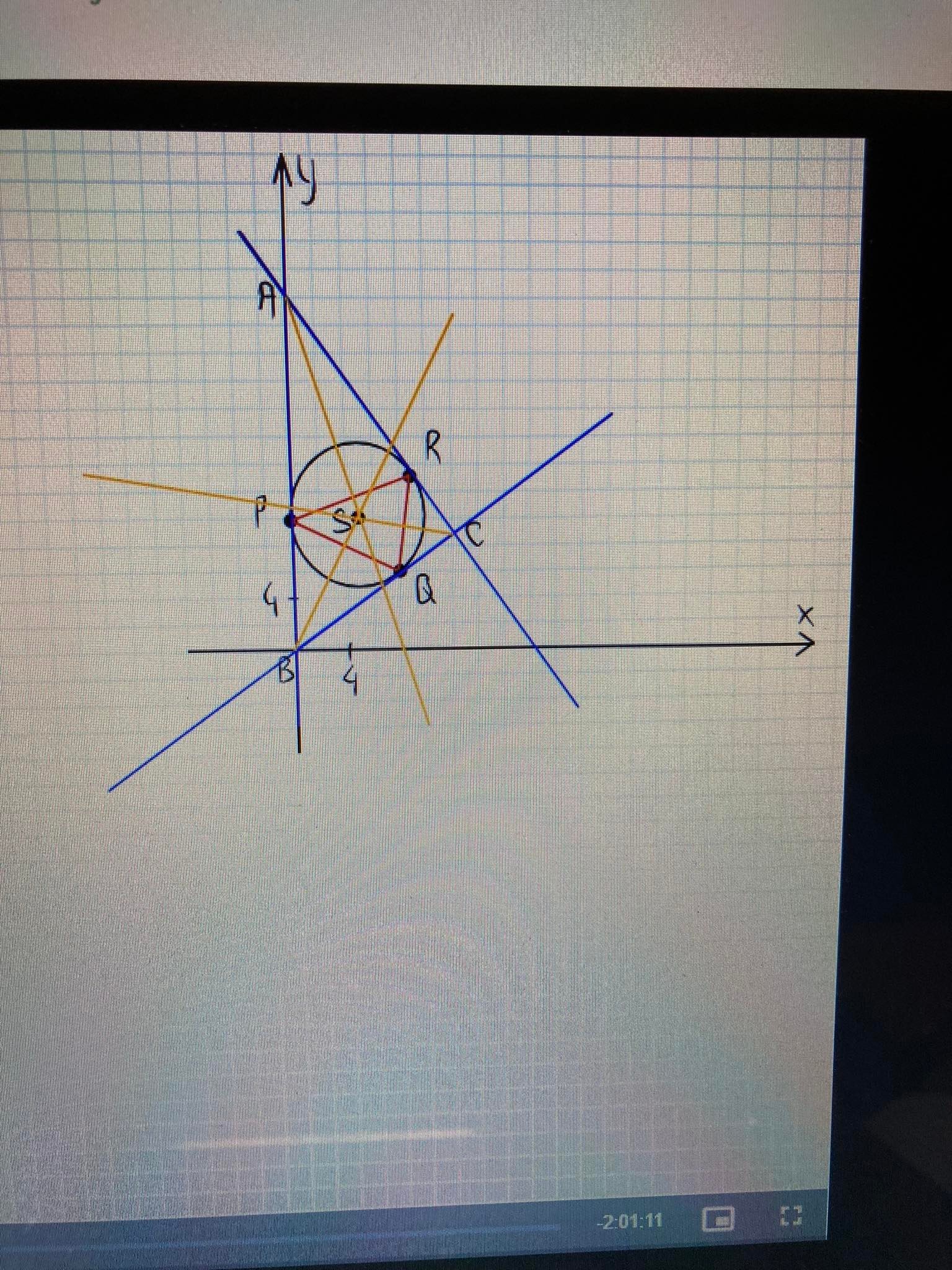
To zadanie było robione na 2 lekcji z geometrii analitycznej. Wystąpiło tam twierdzenie mówiące, że dwusieczne trójkąta ABC to symetralne trójkąta PQR. Czy można by dowieść to twierdzenie odwołując się do twierdzenia o środku okręgu opisanego i wpisanego w figurę? Tzn. wiemy, że środek okręg wpisanego w daną figurę czyli tutaj w trójkąt ABC znajduje się na przecięciu dwusiecznych tej figury, a środek okręgu opisanego na danej figurze, tutaj trójkąt PQR, znajduje się na przecięciu symetralnych tej figury. Czy to wystarczy?

---

Geometria analityczna Dodaj post do ulubionych Poproś o pomoc