Arkusz 11 zadanie 11

Cześć, nie widzę błędu jaki popełniłem w zadaniu. Podstawiłem pod tan2alfa , ale wynik nie zgadza się z odpowiedzią. Co źle zrobiłem ?
Arkusze matematyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie jesteś w stanie w tej prostej, tg(alfa) to kąt nachylenia prostej do osi OX.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale przecież tu poza wzorem tg2alfa został jeszcze użyty wzór tg(alfa-beta), dzięki któremu uzyskujemy współczynnik "a" pomiędzy prostymi, a nie nachylenie do osi OX. Co jest w tym błędnego?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
No w całym tym rozumowaniu.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Mówisz o rozwiazaniu @Mikol?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale skąd wiesz jaki będzie współczynnik kierunkowy dwusiecznej tzn. skąd wiesz pod jakim kątem będzie ona nachylona do osi OX?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tego nie wiem, ale znam tg kąta pomiędzy tymi prostymi i tg połowy tego kąta to chyba powinien być szukany wsp. kier. tej dwusiecznej.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Artur zajrzyj do kart wzorów czym jest współczynnik kierunkowy prostej i czym jest kąt pod którym nachylona jest taka prosta - strona 23 w kartach.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jest to nachylenie funkcji liniowej do osi OX.
Czyli tym sposobem, który proponowałem ja i mikol to czym jest to co nam wychodzi skoro nie jest to równanie tej prostej?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wychodzi takie coś. Czyli właściwie nie wiadomo co to jest za prosta?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak - to jest po prostu błędnie obliczona prosta.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale ogólnie to stwierdzenie: "Pomyślałem że kat nachylenia dwusiecznej do obu prostych jest dwa razy mniejszy niż ich kąt przecięcia się." jest tutaj prawdziwe?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
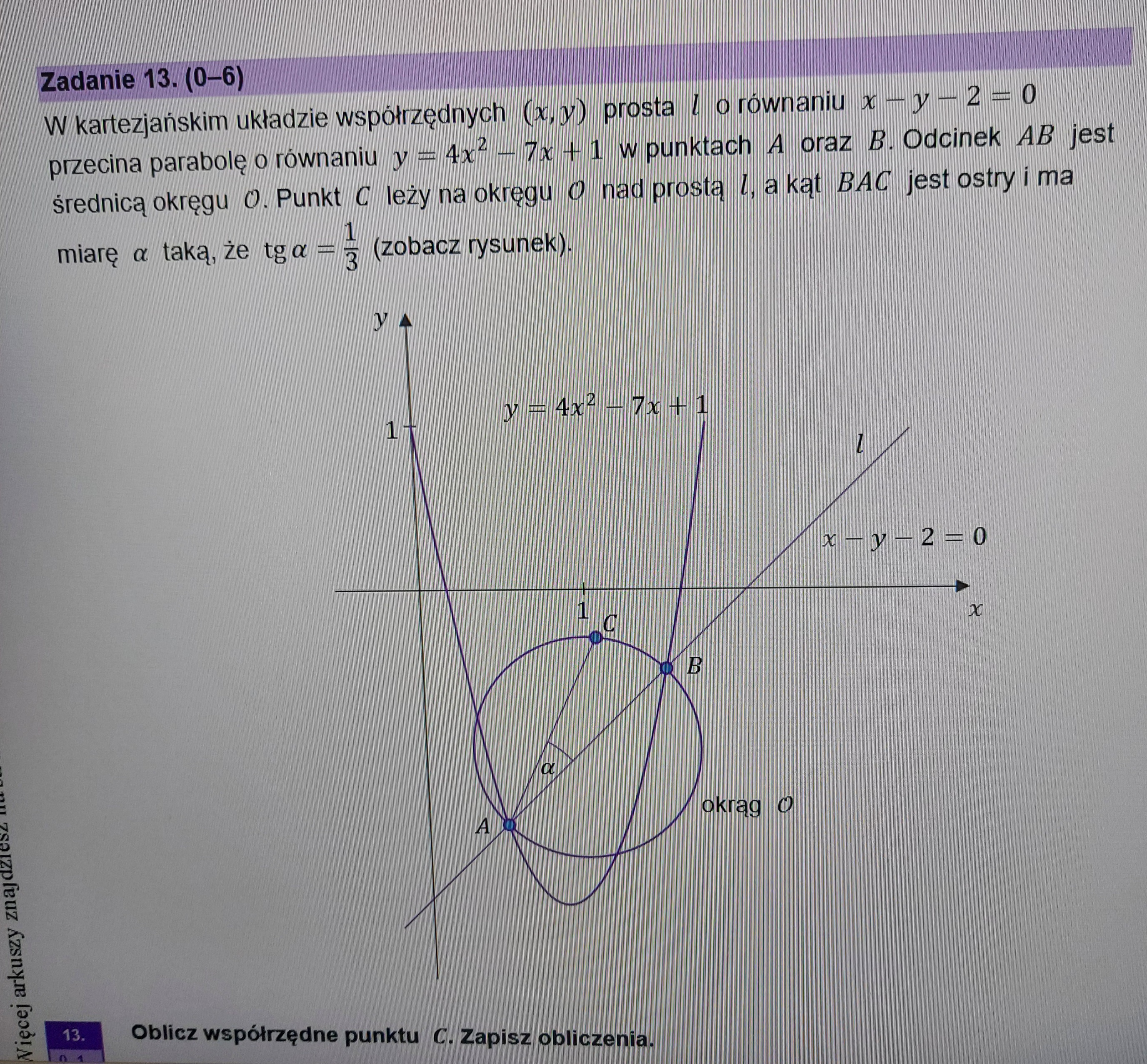
Dlaczego właściwie można w ten sposób z tg różnicy zrobić zadanie 2023.13 a tego, zadania nie można? Jakiej informacji brakuje aby można tak było to robić?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W tym zadaniu wszystko się zgadza, analizujemy nachylenie do osi OX:
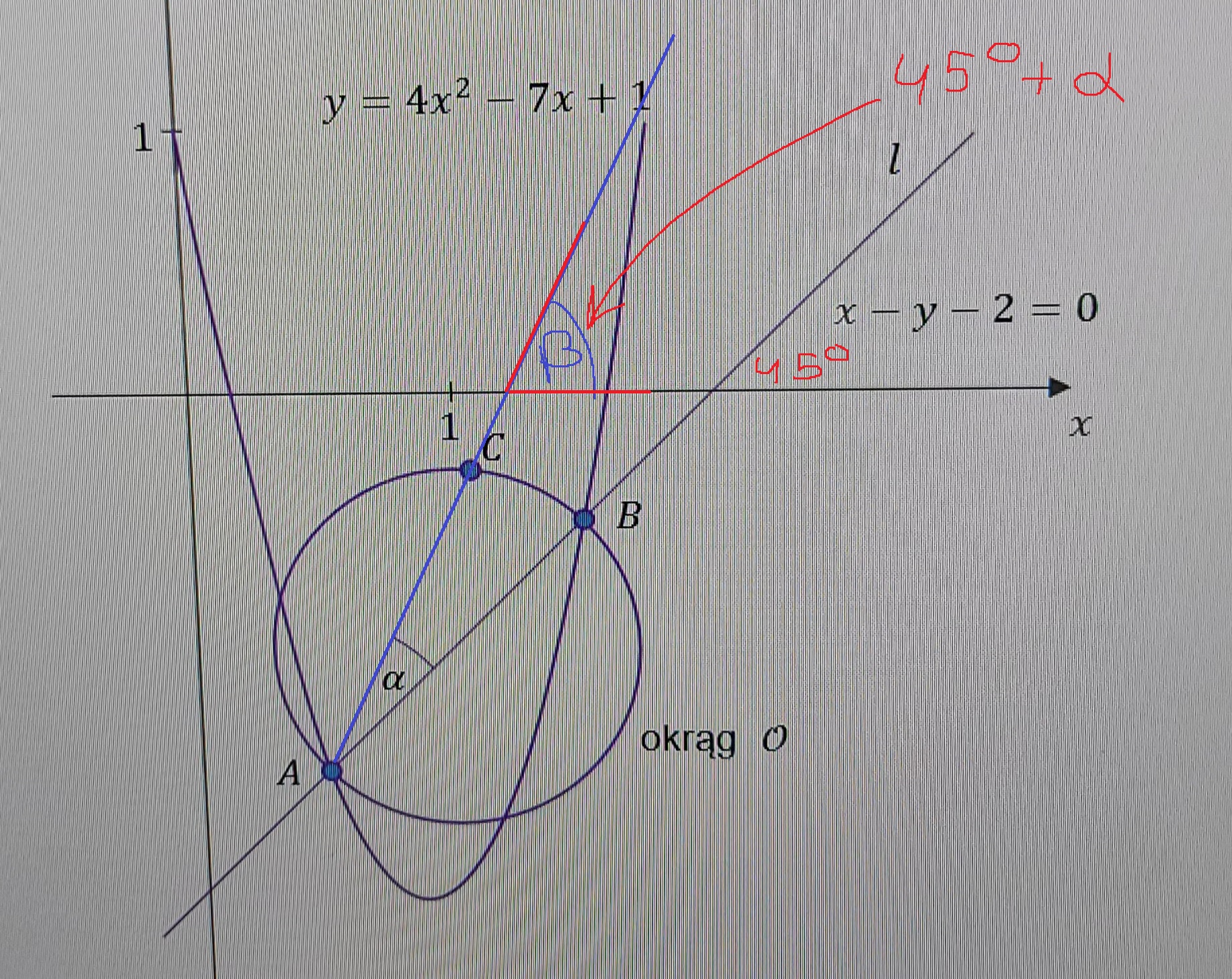
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Mógłbyś wyjaśnić swój tok rozumowania w swoim rozwiązaniu?
To zadanie należy zrobić wykorzystując fakt, że jeżeli punkt P(x,y) leży na dwusiecznej, to jego odległość od obu prostych jest jednakowa.