Dany jest trójkąt równoboczny ABC o boku długości a ...
Dany jest trójkąt równoboczny 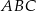 o boku długości
o boku długości  . Punkty
. Punkty 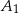 ,
, 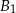 i
i 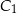 należą do boków
należą do boków 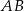 ,
, 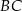 i
i 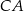 , przy czym
, przy czym 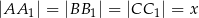 .
.
- Wyraź pole trójkąta
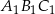 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji.
. Wyznacz dziedzinę tej funkcji. - Wyznacz wartość
 , dla której pole trójkąta
, dla której pole trójkąta 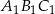 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.

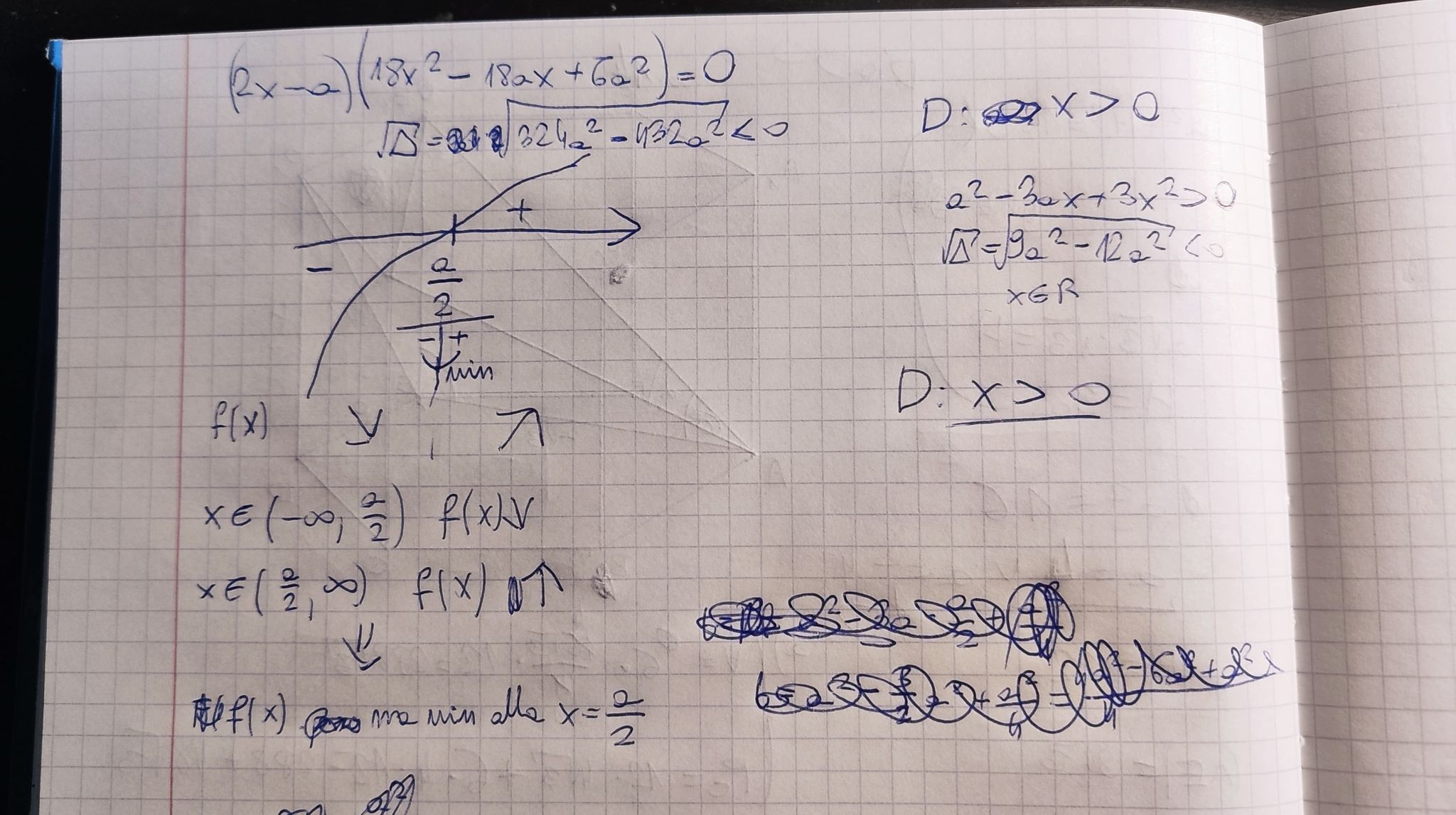
Co w tym zadaniu jest źle ponieważ wychodzi mi sprzeczność jak liczę moje b natomiast niby wszystko jest okej. Wyszedłem od wzoru na pole tr. równobocznego ponieważ z Tw. cos mamy, że wszystkie boki tego mniejszego trójkąta są takie same.
matematyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
okej, już widzę tam zamiast b powinno być b do kwadratu. dziękuję, czyli jeśli wezmę to wyrażenie pod pierwiastek i obliczę to to będzie to poprawne rozwiązanie?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Na pierwszy rzut oka powinno być ok, aczkolwiek sprawdź to :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zwróć uwagę na pierwszą linijkę swojego rozwiązania. Tw. cos: