Arkusz 11 zad 10.2

Ściśle można dojść do tego zapisując sobie zasadę zachowania energii całkowitej dla tego rozpadu - dla ułatwienia można przyjąć, że poczatkowa energia kinetyczna jądra Th-232 była zerowa (energia kinetyczna produktów już zerowa oczywiście nie jest). Jeśli w zapisie zasady zachowania energii całkowitej masy jąder rozpiszemy zgodnie z bilansem masy jądra jako różnicę sumy mas nukleonów i deficytu masy i będziemy pamiętać, że energia wiązania to deficyt masy*c^2, to dojdziemy fakytcznie do wniosku, że energia wiązania substratu bedzie mniejsza niż suma energii wiązań produktów.

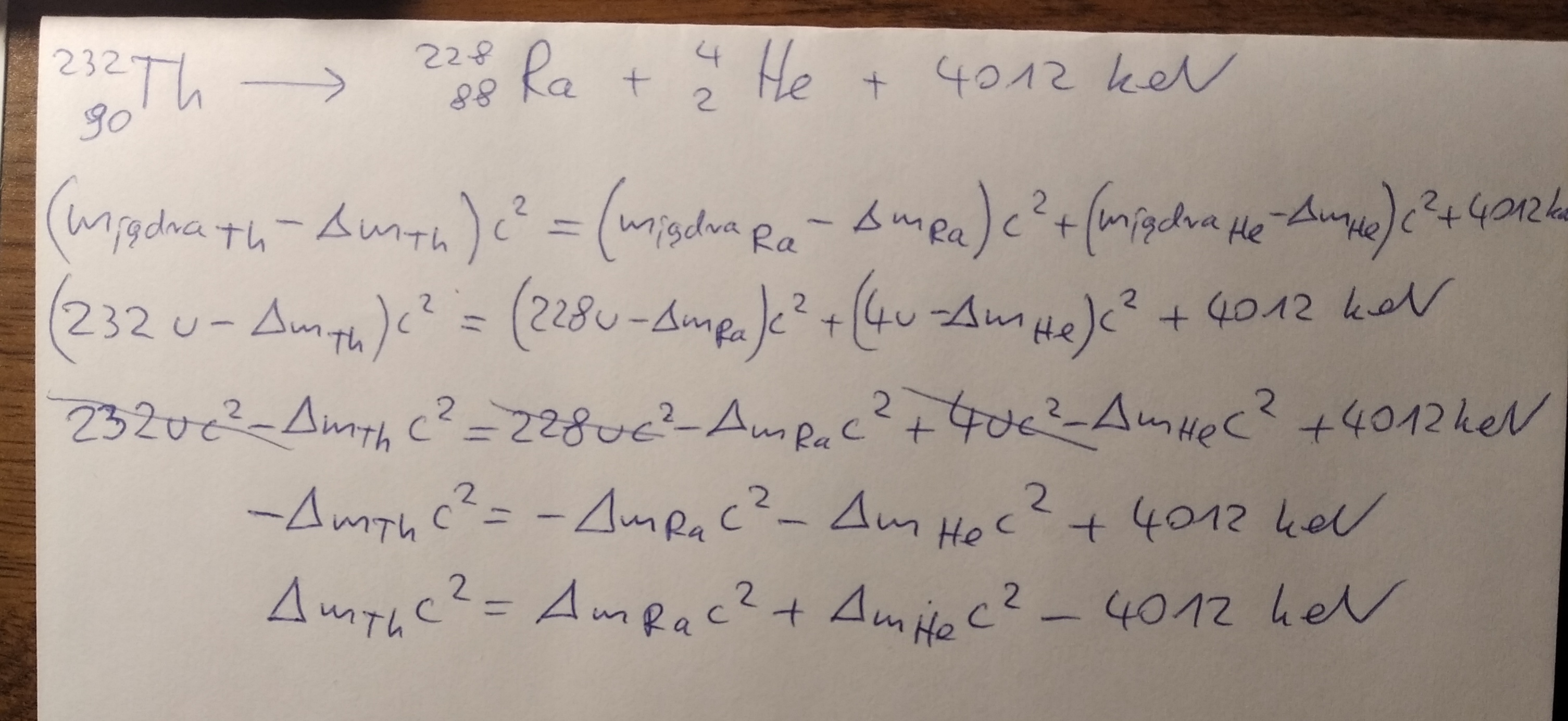
O to chodzi? Czyli energia wiązania jądra toru jest mniejsza od sumy energii wiązań produktów o energię wyemitowaną podczas tego rozpadu i niesioną przez jądro Helu.

Wniosek wyszedł Ci dobry i o to "prawie" chodzi, bo samo początkowe przejście nie jest poprawne, bowiem poczatkowe równanie powinno wyglądać następująco: m_jądraTh*c^2 = m_jądraRa*c^2 + m_jądraHe*c^2 + 4012 keV. I dopiero teraz zapisujemy masy jąder zgodnie z bilansem masy dla jądra, czyli np. dla masy jądra toru będzie to: m_jądraTh = 90*mp + 142*mn - deficyt_Th, i analogicznie dla jądra radu i jądra helu. Wszystkie masy protonów i neutronów się jednak poskracają i ostatecznie dostaniesz takie samo równanie jak masz teraz na kartce, czyli deficyt_Th*c^2 = deficyt_Ra*c^2 + deficyt_He*c^2 - 4012 keV, stąd faktycznie wynika, że energia wiązania toru jest mniejsza niż suma energii wiązań produktów.