Paulina 256 wyśw. 05-05-2022 21:02

Nowa era arkusz 4 zadanie 8


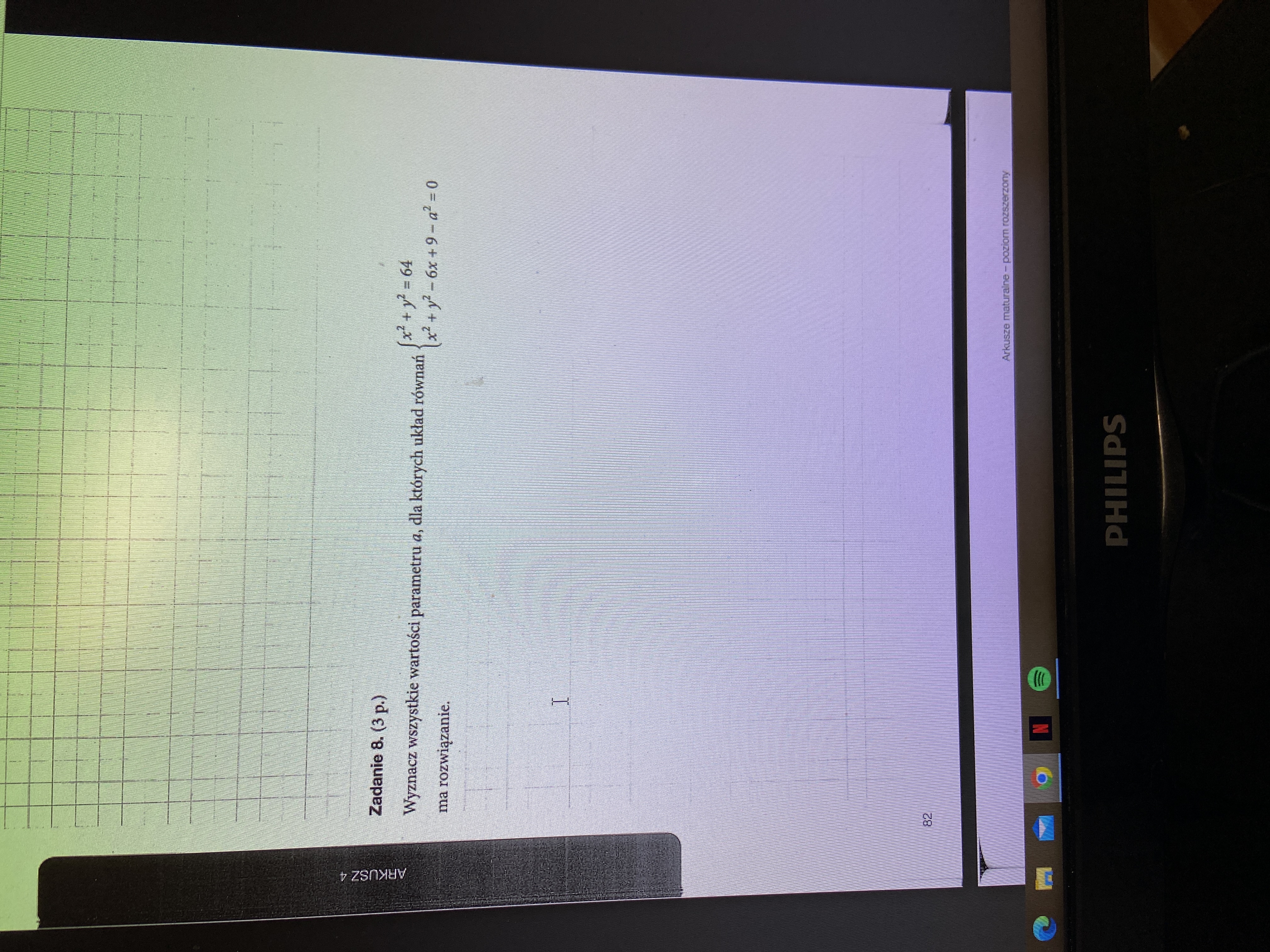
Jak zrobić to zadanie ?

Matematyka matura Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 06-05-2022 03:19

Można zauważyć, że równania w układzie to równania dwóch okręgów o konkretnych środkach i promieniach. Jak dobrze wiemy, dwa okręgi mają wspólny punkt/punkty gdy zachodzi warunek: |r_1 - r_2| <= |O_1O_2| <= r_1 + r_2

Czyli ostatecznie:

1. Zapisać równania jako równania okręgów przekształcając je.

2. Rozwiązać powyższy warunek.