Paulina 425 wyśw. 05-05-2022 21:04

Nowa era arkusz 4 zadanie 9


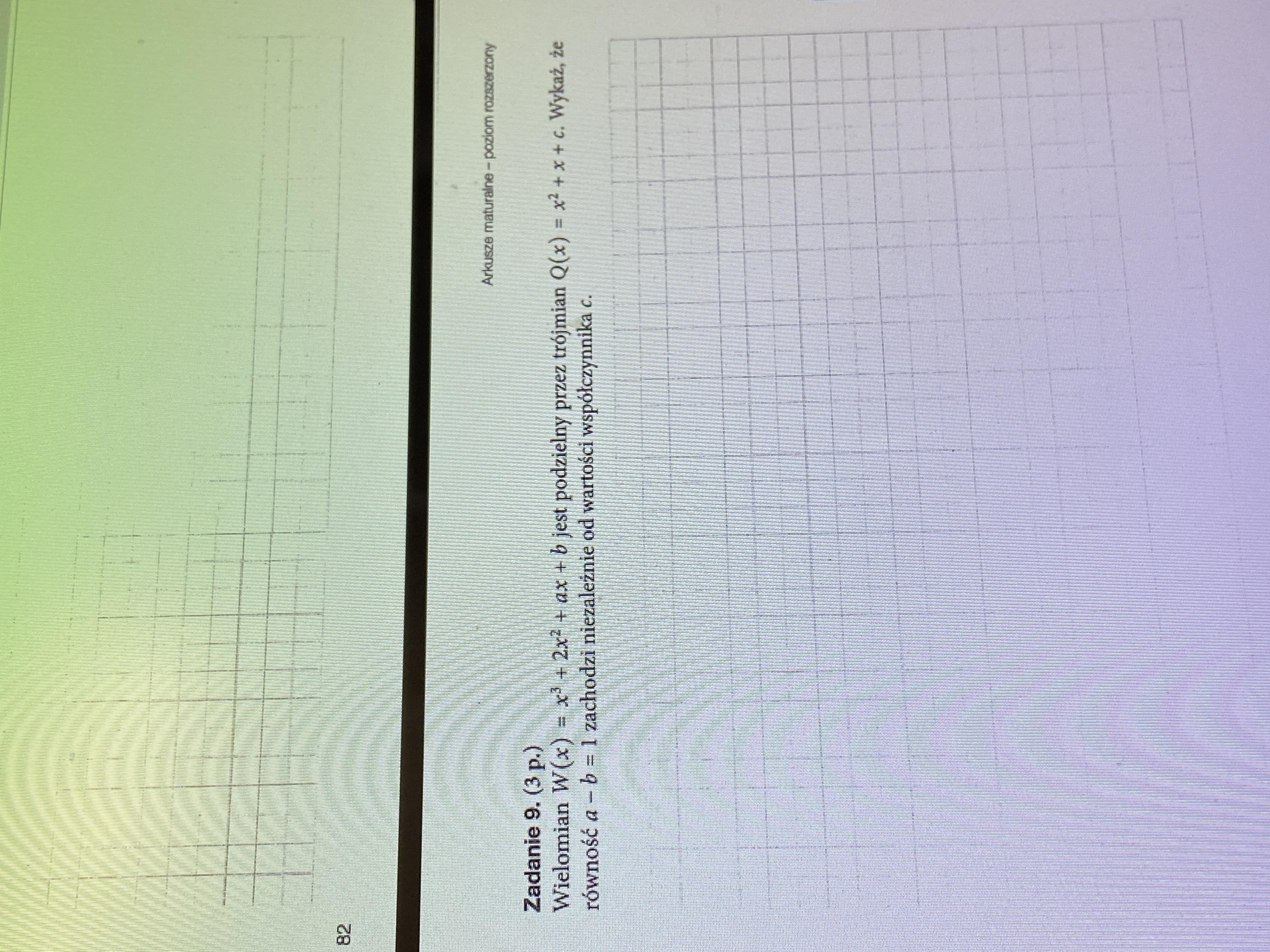
Jak zrobić to zadanie ?

Matematyka matura Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 06-05-2022 03:28

Skoro wielomian W(x) (3 stopnia) jest podzielny przez wielomian Q(x) (2 stopnia) to możemy zapisać, że:

W(x) = (x+d)*Q(x)

Pozostało wymnożyć (x+d) * Q(x) podstawiając pod Q(x) trójmian z polecenia. 

Następnie pozostało porównać współczynniki oryginalnego W(x) z W(x) wymnożonym. 
Zapisując układ równań:

I zapisując:

d=1 oraz a-b = c + d -cd = c + 1 - c = 1 pokazujemy, że a-b=1 nie zależy od współczynnika "c" więc możemy zakończyć nasz dowód.