NE arkusz 6 z.9

Sposób 1: przebieg zmienności i wyznaczenie ZW
Sposób 2: Próbowałem jeszcze drugim sposobem rozbijać to na postać iloczynową za pomocą układu równań, żeby mieć iloczyn dwóch trójmianów kwadratowych, aby potem policzyć delty obu wyrażeń. Niestety układ równań, który tu powstaje nie jest szybki do rozwiązania.
Oba sposoby są przydługawe, może jest jakiś szybszy ?
inny sposób Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli muszę wymnożyć to wszystko co w poleceniu i potem zapisać równolegle (x^2 +bx +c)(x^2 +bx +c), wtedy wymnażam trójmany z niewiadomymi i porównując współczynniki w układzie równań otrzymuję konkretne wartości ?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie musisz wszystkiego wymnażać ani niczego porównywać, wystarczą przekształcenia.
Oczywiście twoim sposobem też by przeszło natomiast nie to miałem na myśli.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
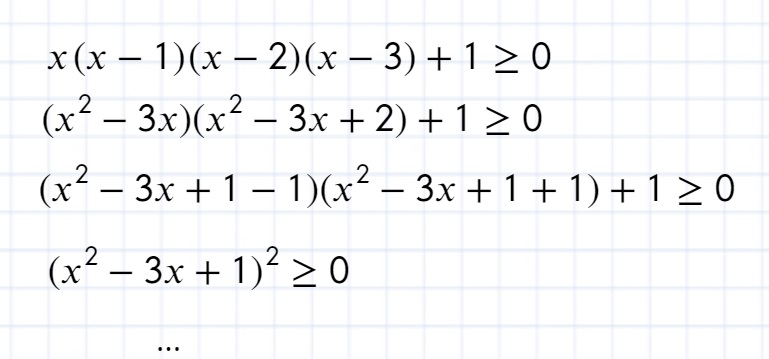
Można to zwinąć do postaci: (x^2-3x+1)^2
Oczywiście nie należy to do najprostszych rozwiązań aczkolwiek przy odpowiednim doświadczeniu można bardzo szybko sobie z tym poradzić.
Na maturze warto poświęcić chwilę na przekształcenia -> jeżeli wypali to zaoszczędziliśmy sporo czasu, z kolei gdy nie pójdzie to wyciągamy armatę w postaci badania zmienności funkcji :)