Strona 328 zadanie 4

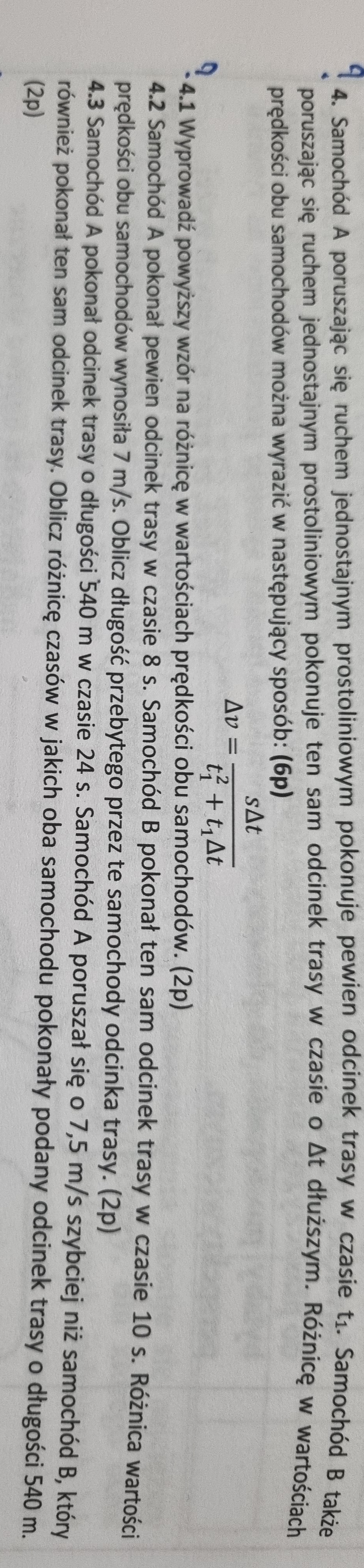
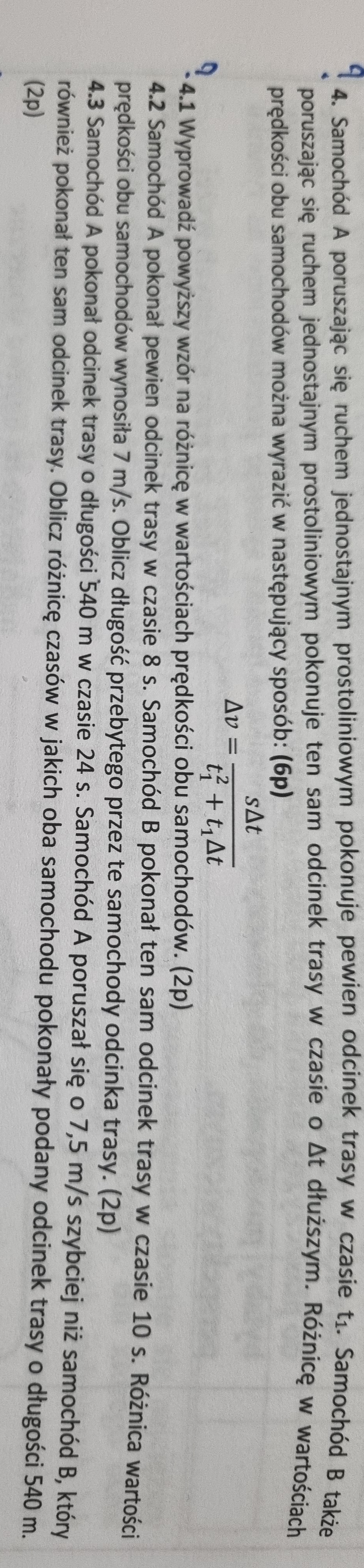
Oba samochody poruszają się ruchem  jednostajnym, więc dla obu obowiązuje następująca zależność między predkością, drogą i czasem: v = s/t. Stąd dla pierwszego samochodu mamy v1 = s/t1, a dla drugiego, który tę samą drogę przebył w czasie dłuższym o deltat, dostajemy: $$ v_2 = \frac{s}{t_1 + \Delta t} $$

Teraz wchodzi już czysta matematyka. Trzeba odjąć od siebie te prędkości, żeby dostać ich różnicę deltav i doprowdzić do takiej postaci jak w treści - w tym celu trzeba będzie sprowadzić te dwie prędkości do wspólnego mianownika i faktycznie dojdziemy do pożądanego wzoru.