natalcia 368 wyśw.
05-12-2022 14:04
zad 12
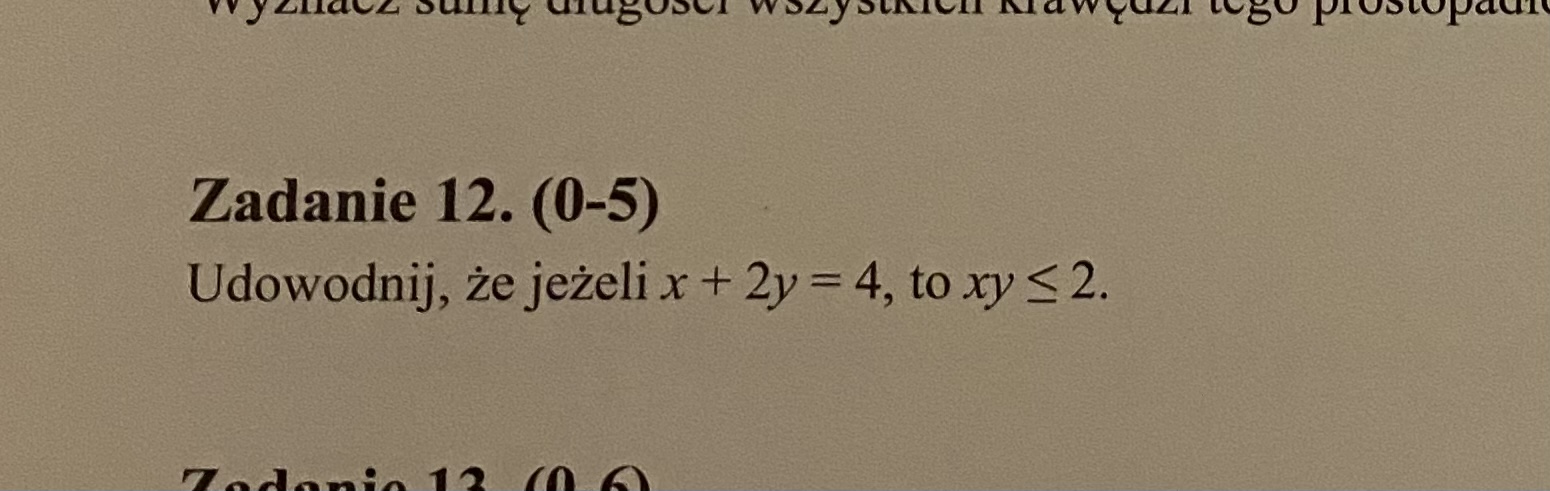
Udowodnij, że jeżeli x + 2y = 4, to xy ≤ 2.
Proszę o pomoc:)
matematyka matura arkusz dowodzenie dowodzenie nierówności Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Tomek
05-12-2022 17:02
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jarosinski
06-12-2022 10:47
Oto rozwiązanie w przypadku liczb dodatnich:
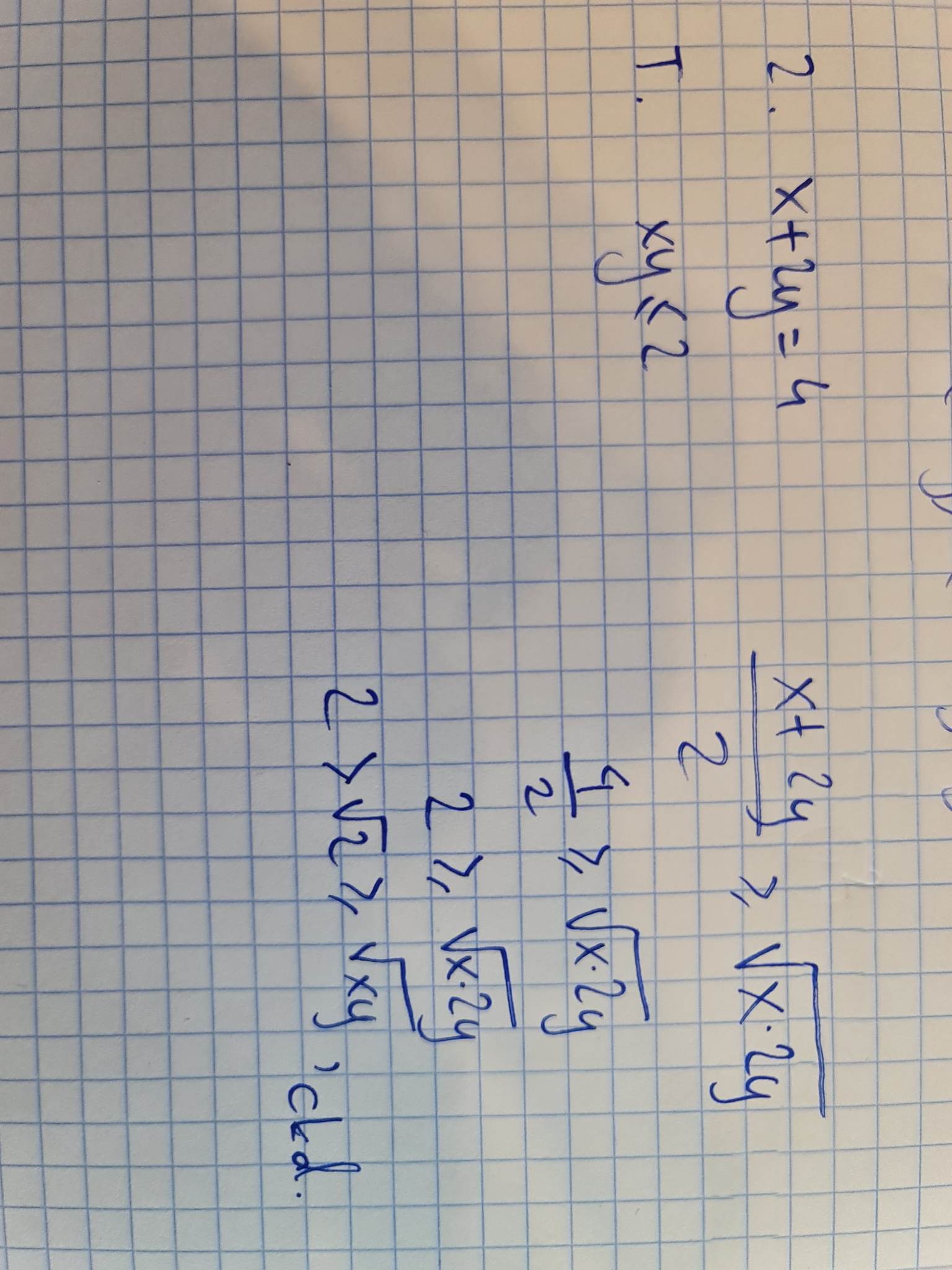
Jeśli natomiast jedna zmienna jest dodatnia, a druga ujemna to teza zachodzi z automatu
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Po przekształceniu dostajemy xy = -2y^2 + 4y
-2y^2 + 4 to funkcja kwadratowa z ramionami idącymi w dół, więc jej najwyższą wartością jest współczynnik q.
Ponieważ xy = -2y^2 + 4y , to najwyższa wartość funkcji -2y^2 + 4y będzie też najwyższą wartością xy