Kiełbasa 651
W urnie są 4 kule białe i 6 czarnych. Losujemy 4 razy po 5 kul i po każdym losowaniu zwracamy je do urny. Jakie jest prawdopodobieństwo, że dwa razy wylosujemy 5 takich kul, wśród których będą 3 kule czarne i 2 białe?
Proszę o rozwiązanie tego zadania.
matematyka schemat Bernoulliego Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jak wyliczyć prawdopodobieństwo sukcesu?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Prawdopodobieństwo czyli:
ilość możliwości na jakie możemy wylosować 3 kule czarne * ilość możliwości na jakie możemy wylosować 2 kule białe
podzielone przez:
ilość wszystkich możliwości na które możemy wylosować 5 kul z 10
Zatem: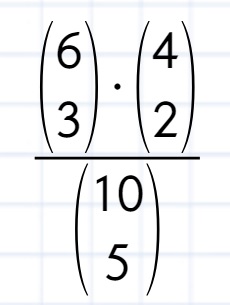
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A czy mógłby wyjaśnić Pan, w jaki sposób i dlaczego wyznaczenie prawdopodobieństwa sukcesu w tym wypadku wygląda akurat tak? Zastanawia mnie to dzielenie przez 10 po 5
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Którą dokładnie operacja jest nie jasna? Każde działanie zostało opisane w mojej odpowiedzi, sprecyzuj swoje pytanie.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wskazówka: Schemat Bernoulliego pozwala obliczyć nam prawdopodobieństwo k-sukcesów w n-próbach.
Naszym sukcesem jest wylosowanie dwa razy (k) kombinacji 3czarne 2białe w czterech próbach (n).
Jedyne czego nam brakuje aby wykorzystać wzór Bernoulliego jest prawdopodobieństwo sukcesu w jednej próbie.
Wystarczy zatem obliczyć prawdopodobieństwo wylosowania 3 kul czarnych i 2 kul białych z urny. Następnie wyliczone prawdopodobieństwo podstawiamy do wzoru :)
W razie problemów proszę śmiało pisać.