Zadanie domowe 6 cz. I Zad. 1-5
1. Podaj ZW
2. Narysuj wykres
3. Wyznacz wzór funkcji (sin)
4. Wyznacz k, dla którego równianie ma 4 różne rozw.
5. Wyznacz k dla których równanie ma 4 różne rozw.
Dzień dobry, potrzebuję wskazówek do zadań, trygonometria idzie mi fatalnie.
Zad.1 Podaj ZW.
a)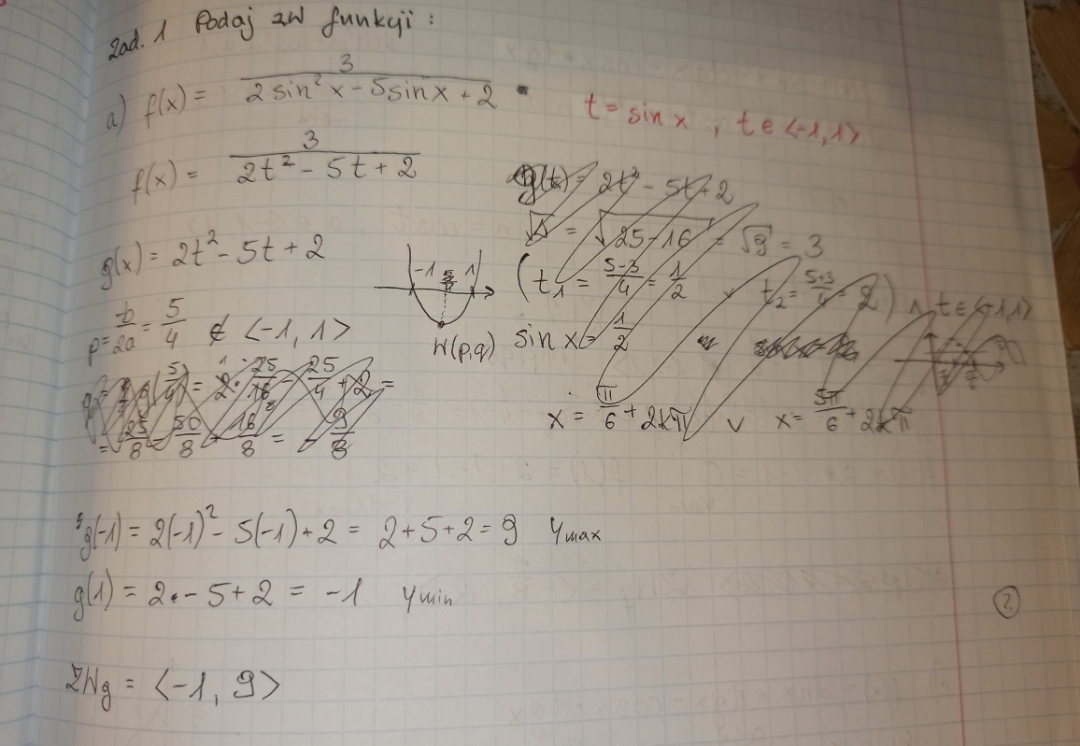
Nie wiem co teraz zrobić, skoro wyznaczyłam już ZW mianownika.
b)
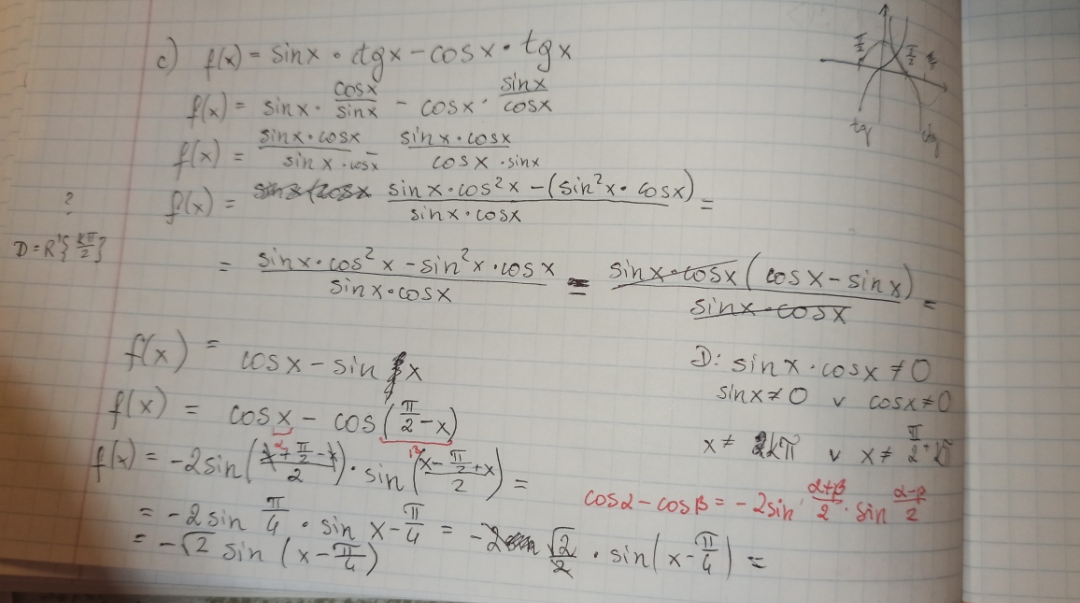
Ten podpunkt zrobiłam, ale wyszedł mi zły wynik, bo nie wiem skąd wzięła się dziedzina D=R-{kπ/2} (moja wyszła inaczej)
c)
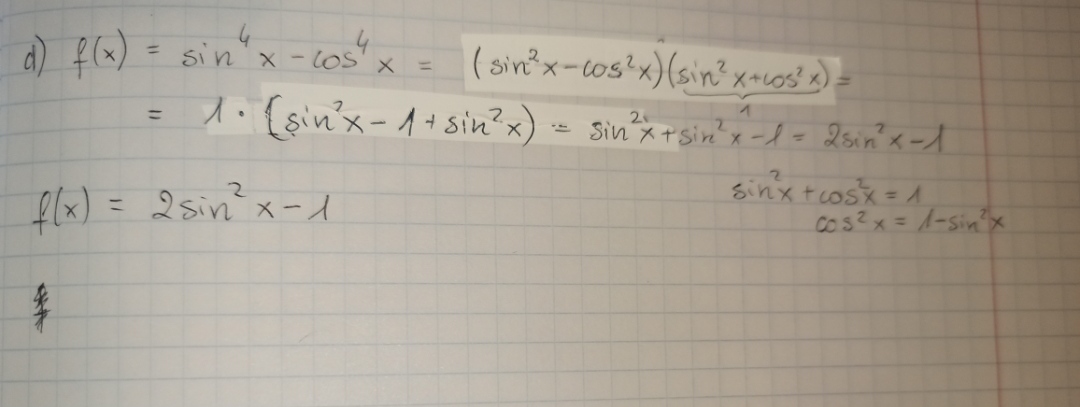
Tutaj generalnie utknęłam. Mam zrobić z tego równanie 2sin²x=1?
Zad.2 Wykonaj wykres

Zupełnie nie rozumiem tego, co jest w odpowiedziach. Wiem z jakich wzorów powstały, ale nie rozumiem jak z -sin²x+cos²x ma powstać cos2x, tak samo z sin²x-cos²x=-cos2x.
Do tego nie wiem kiedy tu przedziały mają być otwarte, a kiedy zamknięte np. sinx>0 jest w (0;π/2), ale w odpowiedziach jest <0:π/2).
Zad. 3

Tutaj utknęłam.
Zad. 4

Co mam zrobić z a=-2?

Tutaj nie mogę kontynuować, bo nie jestem w stanie wyznaczyć poprawnego b.
Zad. 5

Tu mi coś ewidentnie nie wyszło, ale nie wiem jak to inaczej zapisać.
Dziękuję za pomoc
Matematyka rozszerzona trygonometria Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ten podpunkt zrobiłam, ale wyszedł mi zły wynik, bo nie wiem skąd wzięła się dziedzina D=R-{kπ/2} (moja wyszła inaczej)
Skoro mamy funkcję ctg oraz tg to musimy zrobić założenia:
sinx != 0 i cosx != 0
Stąd wynika wskazana przez ciebie dziedzina.
c) Wykonaj podstawienie i t=sinx z ograniczeniami i rozwiąż jak poprzednie przykłady.
Zad 2:
Zupełnie nie rozumiem tego, co jest w odpowiedziach. Wiem z jakich wzorów powstały, ale nie rozumiem jak z -sin²x+cos²x ma powstać cos2x, tak samo z sin²x-cos²x=-cos2x.
Z karty wzorów:
cos2x = cos²x-sin²x
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zad. 3
W kryteriach to zadanie jest rozwiązane szczegółowo. W którym etapie pojawia się problem, co konkretnie jest niezrozumiałe?
Zad. 4
Co mam zrobić z a=-2?
Nic :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zad 5.
Pod tym linkiem znajdziesz rozwiązanie z wyjaśnieniem :)
https://forum.szkolamaturzystow.pl/wpis/1603392972-576-kurs-maturalny
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
a) Wiesz, że mianownik przyjmuje wartości: [-1, 9]
Oczywiście zera nie może przyjąć więc dzielimy sobie ten przedział na dwa:
[-1, 0) oraz (0, 9]
W liczniku mamy 3. Jeżeli podstawimy -1 pod mianownik to będziemy mieli wartość funkcji = -3
Idąc w kierunku zera (z mianownikiem) np. podstawiając -1/2 schodzimy w dół ponieważ 3/(-1/2) = -6 zatem idąc w kierunku zera którego nie osiągniemy wiemy że funkcja przyjmuje na pewno wartości z przedziału [-niesk, -3].
Analogicznie sprawdzamy drugi przedział:
Jeżeli za mianownik podstawimy 9 uzyskamy wartość 1/3, kierując się w stronę zera uzyskujemy wartości coraz większe np.
3/(1/1000) = 3000 zatem finalnie uzyskamy wartości od 1/3 do nieskończoności.
Zatem ostateczny zbiór wartości naszej funkcji to: (-inf , -3] oraz [1/3, + inf)