Pawi 839 wyśw. 16-02-2023 08:34

2022.C.14

Dane są okrąg o1 o równaniu (x−6)2+(y−4)2=98 oraz okrąg o2 o promieniu 2√5.

Środki okręgów o! i o2 leżą po różnych stronach prostej k o równaniu y=−3x−6, a punkty wspólne obu okręgów leżą na prostej k.

Wyznacz równanie okręgu o2.

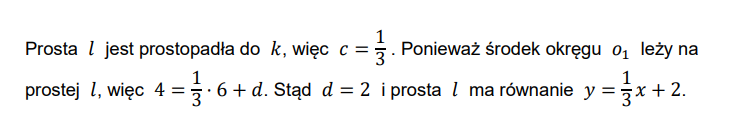
Czy mógłby ktoś mi wytłumaczyć czemu prosta l jest prostopadła do prostej k? Jak do tego dojść?

geometria analityczna Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
hgd4 16-02-2023 14:58

Prosta jest prostopadła, bo przechodzi przez środki obu okręgów (ta prosta przechodzi przez prostą y = -3x -6, więc nie ma innej opcji, żeby te proste były inne niż prostopadłe.

Żeby do tego dojść możesz:

1) wpierw wyznaczyć współczynnik a prostej prostopadłej

2) d znajdziesz poprzez podstawienie punktu środka S(6,4) do równania prostej