Zadanie domowe nr 21, część 1, zad. 4.1, str. 368
Dzień dobry. Mam pytanie.
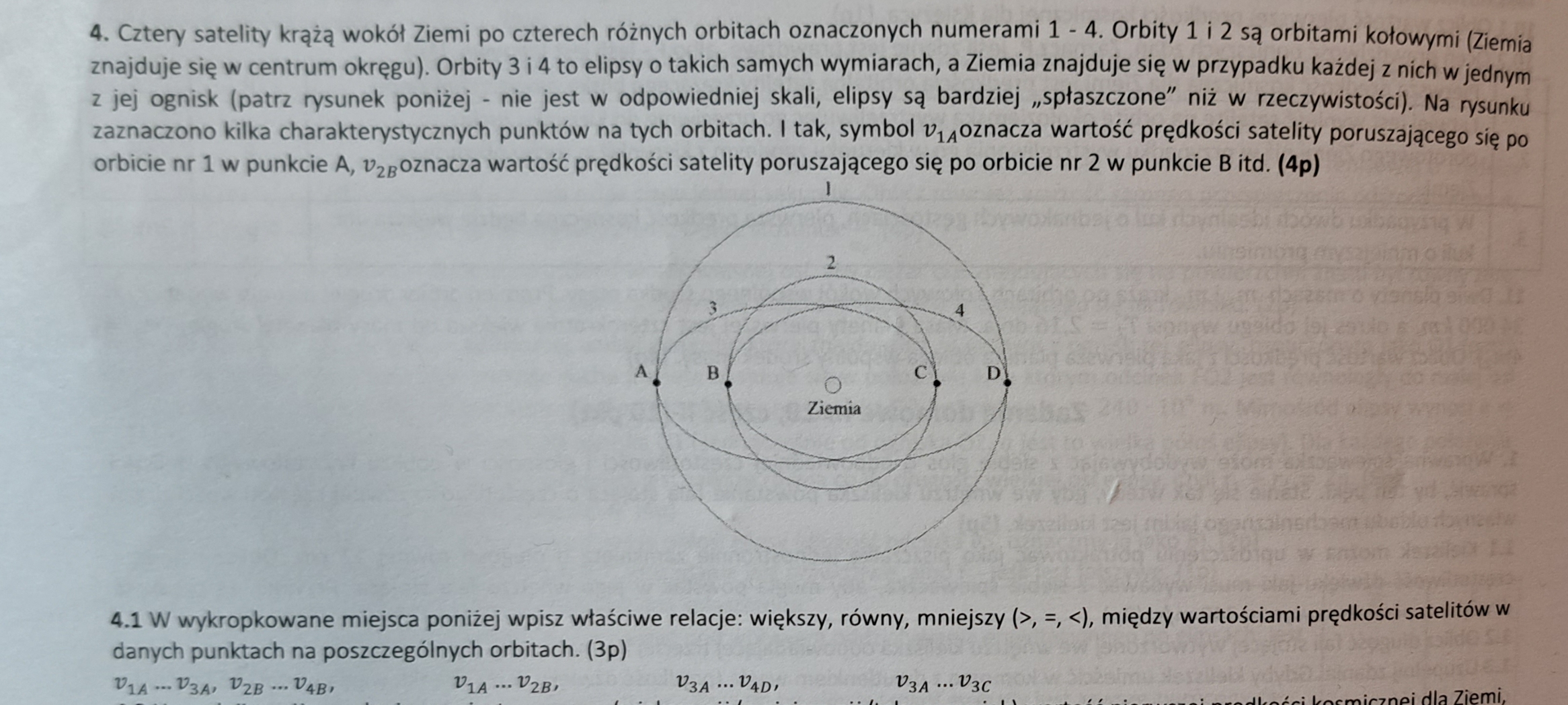
Bo w odpowiedziach jest, że v2B<v4B.
Czy nie powinno być odwrotnie (v2B > v4B)?
Fizyka grawitacja kosmologia satelita Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Okej, obejrzałem jeszcze raz wideo z lekcji, ale nadal trochę nie rozumiem.
Nadal myślę, że v2B żeby poruszać się po orbicie kołowej musi być większe niż v4B w perycentrum, bo ta elipsa jest wewnątrz okręgu i gdy np. ciało ma się poruszać po okręgu, to musi być jakby "wyrzucane" z elipsy, a do tego potrzebuje większej prędkości (na zajęciach był przykład, gdzie to okrąg znajdował się wewnątrz elipsy i wtedy rozumiem, że vp>vorb - zdjęcie).

- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ok, muszę tutaj przyznać, że niestety rysunek podany w treści zadania 4.1 jest po prostu mylący - ta orbita nr 4 w rzeczywistości powinna być "szersza", czyli okrąg nr 2 powinien być w jej wnętrzu i wtedy wszystko się zgadza. Dlatego właśnie wspomniałem wcześnie, że te elipsy nie są niestety zbyt dokładnie narysowane i należy polegać tutaj na samej treści, a nie rysunku. Teraz natomiast zwróciłeś mi na to szczególną uwagę, że ten rysunek koniecznie powinien być zmodyfikowany tak, aby nie wprowadzał właśnie w błąd. Przepraszam za tę niedokładność i dziękuję za zwrócenie na to mojej uwagi! Więc podsumowując - na rysunku to orbita kołowa nr 2 powinna być "wewnątrz" elipsy i wtedy nie powinno już być żadnych wątpliwości ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Okej, bardzo dziękuję ;)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jest ok. Zauważmy, że v4B to prędkość w punkcie B, gdy satelita znajduje się w perycentrum (może elipsy na rysunku nie są idealnie sporządzone i nie widać dokładnie, że jest to punkt najbliższy Ziemi na tej orbicie, ale jest to napisane w treści), a zatem w tym punkcie ma on większą prędkość niż prędkość, którą posiadałby w tym punkcie, gdyby poruszał się po orbicie kołowej (a taką predkością jest właśnie v2B), dlatego v4B > v2B. To jest dokładnie ten sam przypadek co dwa zadanka, które rozważaliśmy na zajęciach pod rząd.