2012C.1., strona 42,„Kurs maturalny - fizyka”
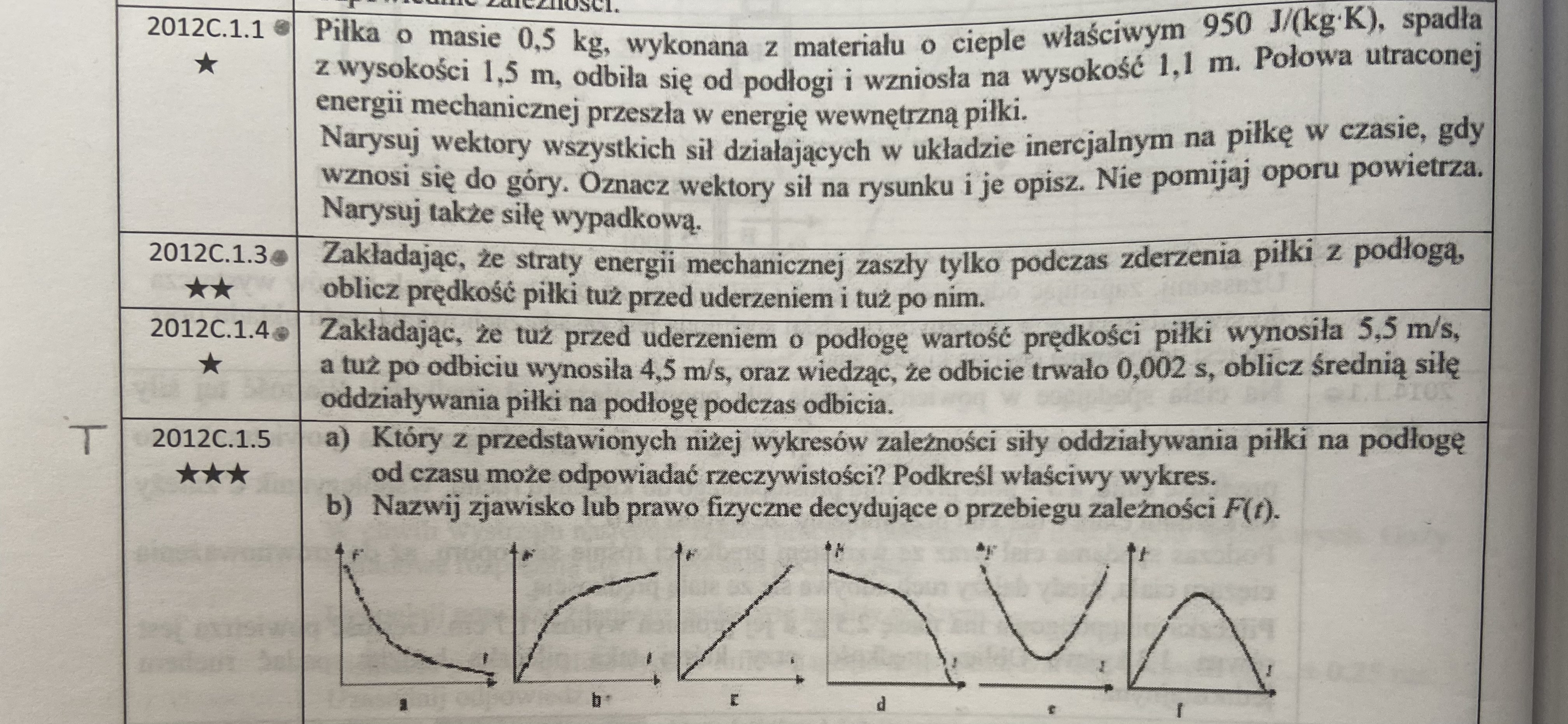
Nie wiem w jaki sposób rozwiązać zadanie 2012C.1.5. Próbowałem w jakiś sposób wykorzystać wzór F = delta p / delta t, ale nie wiem jak dojść do tego, że funkcja będzie miała kształt taki jak na rysunku f. Nie wiem też jak rozumieć odpowiedzi do punktu b) odnoszące się do sprężystości piłki i prawa Hooke'a - o czym ono mówi?
fizyka dynamika Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wzór F = deltap/deltat niestety tutaj nie pomoże. Pomóc może natomiast potraktowanie tej piłki np. jak gdyby była to jakaś sprężyna odbijająca się od podłoża. Czyli powiedzmy, że mamy sprężynę ułożoną pionowo, która nie jest ani wydłużona, ani ściśnięta i opada ona swobodnie w dół, a następnie uderza w podłoże. Zauważmy, że dolna część sprężyny musi się wtedy zatrzymać i sprężyna w pierwszej fazie ulegnie ściśnięciu, następnie osiągnie moment, w którym jej długośc będzie minimalna (maksymalne ściśnięcie), a następnie zacznie się wydłużać i w końcu oderwie się w całości od ziemi. Analogiczny proces ma miejsce podczas odbicia się piłeczki od ziemi. I teraz wiemy, że sprężyna w momencie zderzenia oddziałuje z pewną siłą na podłoże i ta siła jest tym większa im większe jest ściśnięcie tej sprężyny (zgodnie ze wzorem Fs = k*x, im większe x, czyli odkształcenie sprężyny, tym większa jest siła z jaką ta sprężyna oddziałuje na połączone z nią ciało - tu jest nim podłoże). A zatem na początku zetknięcia z podłożem ta siła jest minimalna, potem rośnie, w momencie gdy sprężyna jest maksymalnie ściśnięta osiąga maksimum, a potem znów spada - i taką zależność siły od czasu mamy przedstawioną na wykresie f. Stąd też odpowiedź b) to np. po prostu sprężystośc piłki. Alternatywną odpowiedzią byłoby prawo Hooke'a, które formalnie mówi o tym co opisałem powyżej, natomiast samo prawo Hooke'a jako takie wypadło z matury, więc używanie tej nazwy nie jest konieczne ;)