Zad dom. 4 cz. I, zad 2, pod. e)

A czy 7 dzieli 75? :)

powołujemy się na twierdzenie o pierwiastkach wymiernych wielomianu które mówi, że: Jeśli wspołczynniki wielomianu są całkowite( dlatego rozpatrujemy tylko całkowite "m" ) to pierwiastków należy szukać wśród liczb postaci p/q gdzie p jest dzielnikiem wyrazu wolnego( u nas 75) a q dzielnikiem wyrazu najwyższego stopnia ( u nas 1) dlatego szukamy tych pierwiastków wśród dzielników 75 

jeśli 75 rozłożymy na czynniki pierwsze to otrzymamy 3 5 5  dlatego sprawdzamy w(3) i w(5)

Ale w moim rozumowaniu ani razu nie powołuję się na to twierdzenie. Kryteria się na to twierdzenie powołują, a tak na prawdę nie można się na nie powołać ponieważ m może być dowolne.

Żeby być dokładnym: to możemy powołać się na to twierdzenie ale wtedy musimy założyć że m jest całkowite, a tym samym odrzucamy wszystkie niecałkowite m'y np. -(268/49)

Sprzeczność wynika z samego twierdzenie o wymiernych pierwiastkach wielomianu. To twierdzenie zakłada, że wielomian ma współczynniki całkowite. Zatem z tego twierdzenia wyliczy się tylko całkowite "m"

Rozumiem, ale to że w kryteriach użyto tego twierdzenia nie znaczy że ja muszę go użyć. W moim rozwiązaniu wyliczam m'a dla x=7 będącym miejscem zerowym - nie używam tego twierdzenia, nie mam żadnych założeń co do m'a. Rozumiem że kryteria odrzucają to rozwiązanie bo w kryteriach zostało użyte to twierdzenie ale użycie go nie jest wymagane.

Możemy nawet wyznaczyć wzór na m:

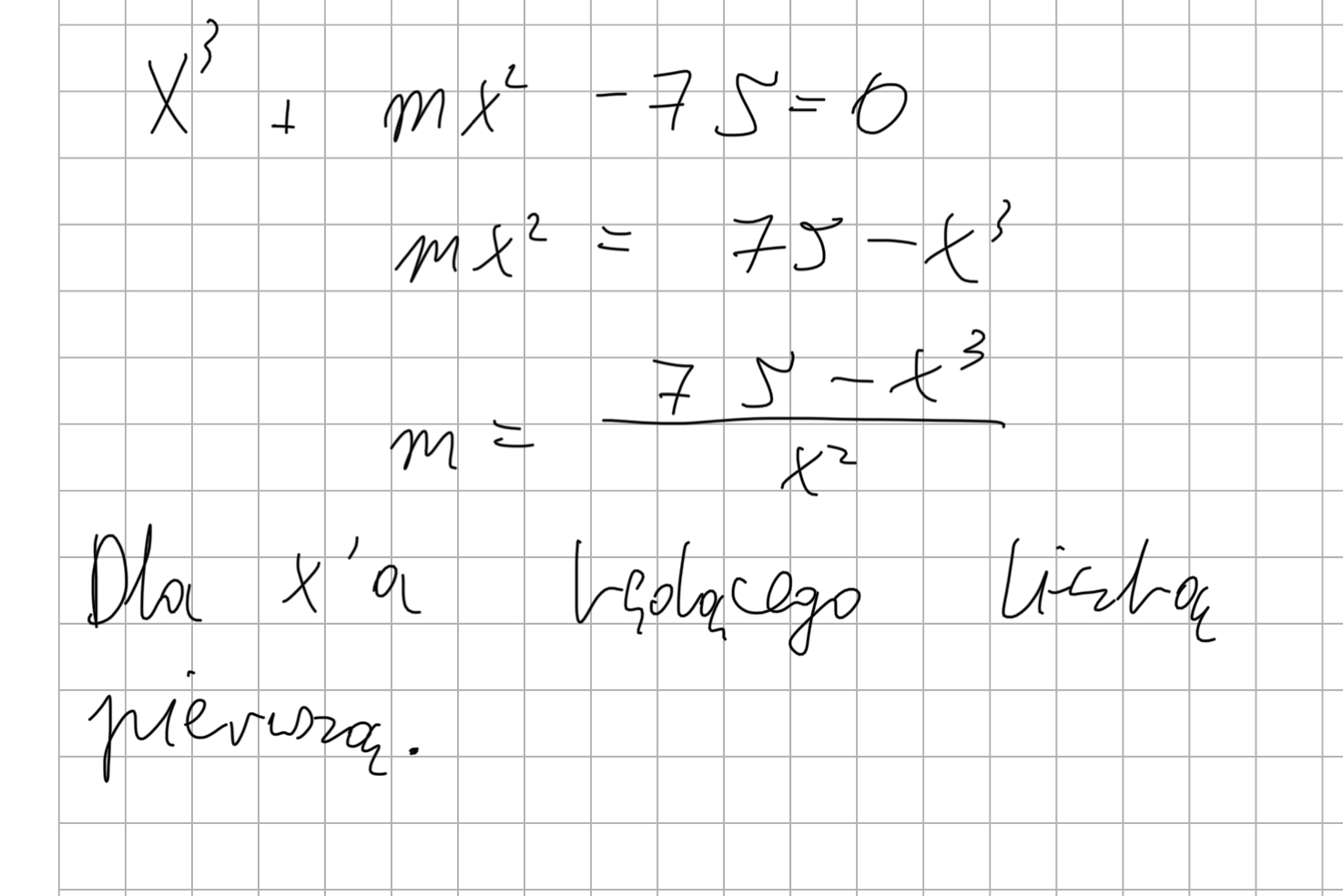
I moim zdaniem ten wzór na m'a jest poprawnym rozwiązaniem.

Dlaczego kryteria nie biorą pod uwagę tego przypadku kiedy m nie jest całkowity?

Tak, oczywiście masz rację :)

Czyli kryteria do tego podpunktu są błędne? W sumie to podpunkt jest błędnie napisany bo nie ma "oczywistego" sposobu jak go rozwiązać.

Żeby naprawić ten podpunkt wystarczy dodać: "załóż że m należy do całkowitych."

Tak dokładnie, należy dodać, że m należy do C