michal 301 wyśw. 26-03-2023 18:18

Optymalizacja w geometrii



Wydaje mi się, że te odcinki (a i b) będą równe i wtedy pole będzie największe, nie umiem tego udowodnić i nie wiem co dalej z tym zrobić

matematyka zadanie geometria Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 29-03-2023 08:54

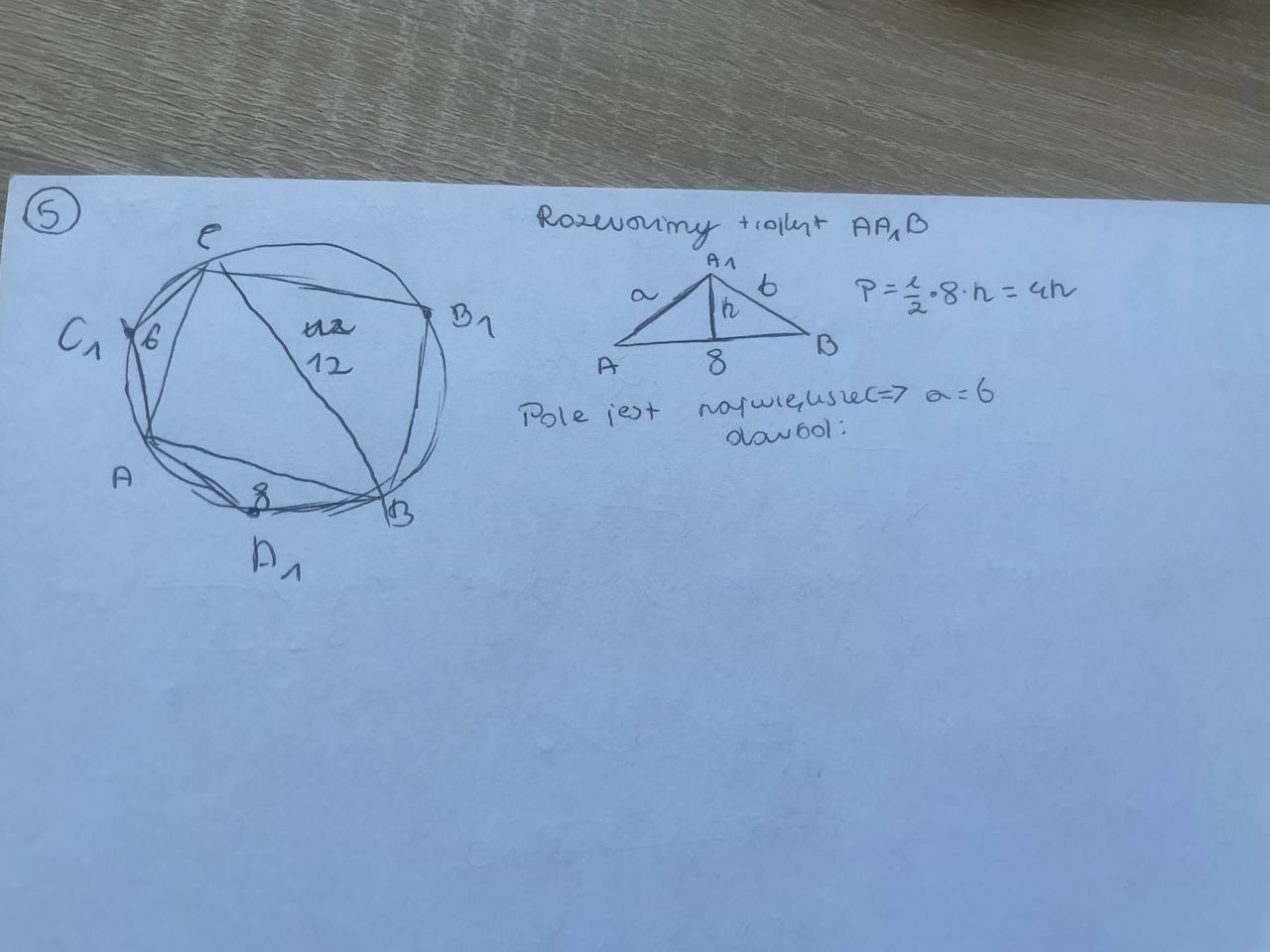
Pole tego sześciokąta składa się z pola trójkąta ABC, które jest stałe oraz z trójkątów AA1B, BB1C oraz CC1A. Zatem pola tych trójkątów AA1B, BB1C oraz CC1A muszą być największe. Te trójkąty mają stałe podstawy i ich pola będą największe jeśli ich wysokości będą maksymalne. A to się stanie wtedy jeśli będą równoramienne.