martyna21 2362 wyśw. 29-03-2023 16:45

Matura matma

Powierzchnia magazynowa jest prostokątną działka  ogrodzona płotem. W ogrodzeniu jest zamontowana brama wjazdowa szerokości 6 metrów. Długość płotu do którego nie wlicza sie szerokości bramy ma wynieść 434 metry. 

Podaj wzór i dziedzinę funkcji opisującej zależność pola tego prostokąta od długości x boku. Oblicz wymiary tej z rozważanych działek, która ma największe pole i oblicz to największe pole. Zapisz obliczenia. Prosze o pomoc i wykonanie. Mam tylko ze 2x+2y=428 i ze wtedy y=214-x ale mam problem z zapisaniem pola przez ta bramę… ja bym zapisała P= x(214-x) ale w odpowiedziach jest inaczej i nie wiem gdzie jest błąd.

Matura matma Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 31-03-2023 19:09

Dlaczego 2x+2y=428 skoro długość płotu do którego nie wlicza się szerokość bramy ma wynieść 434 metry?

martyna21 01-04-2023 13:37

No tak, dlatego 2x + y + y- to 6 m w których jest brama =434 metry

jarosinski 01-04-2023 22:33

Skoro działka jest prostokątna czyli mamy boki: x, x, y, y to obwód prostokąta wynosi 2x+2y, skoro długość płotu bez bramy to 434 metry to razem z płotem obwód działki wyniesie 440 metrów a nie 428 metrów.

martyna21 03-04-2023 14:12

A jak wtedy zapisać wzór na pole bez tej bramy?

jarosinski 04-04-2023 00:42

Wyślij proszę kryteria z odpowiedzi.

martyna21 04-04-2023 18:08


jarosinski 17-04-2023 22:00

1. Skoro długość płotu do którego nie wlicza się szerokość bramy ma wynieść 434 metry i długość bramy ma szerokość 6 metrów. To obwód naszej działki wynosi 434 + 6 = 440 metrów. Zatem 2x + 2y = 440 => x + y = 220 => y = 220-x

2. W związku z tym pole możemy obliczyć: P = x*(220-x)

3. Dziedzina to (0, 214) ponieważ w sytuacji gdy musimy mieć umieszczoną bramę to bok działki nie może być mniejszy od 6 (szerokość bramy).

Spójrz: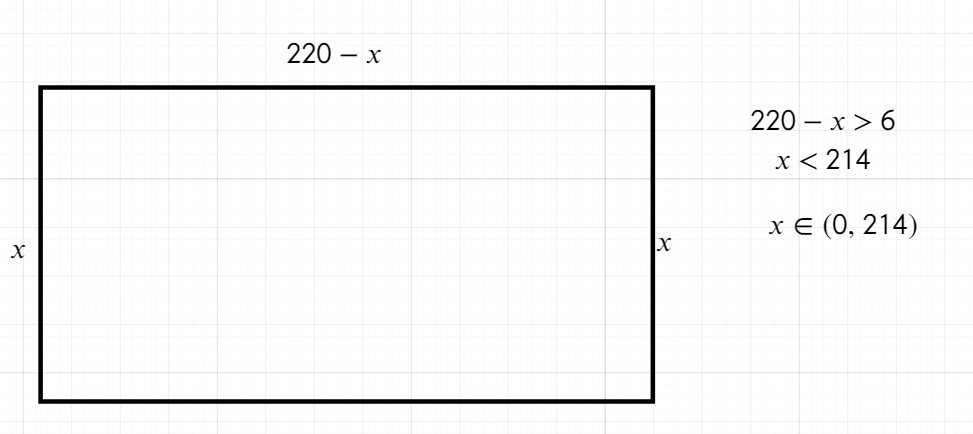 

4. Pozostało znaleźć maksimum tej funkcji w podanym przedziale :)