Zadanie 6

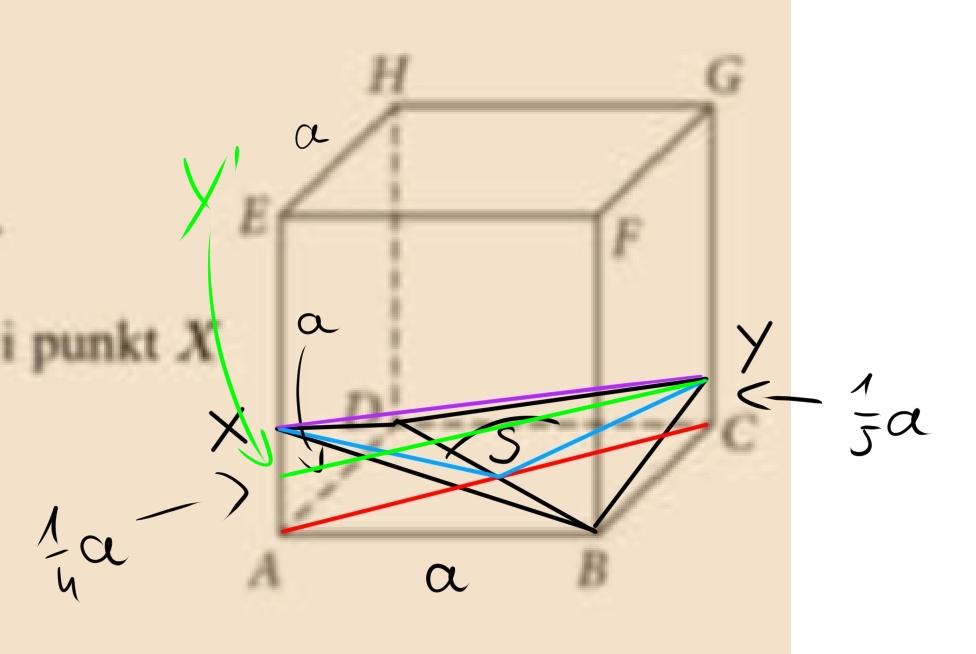
Najpierw polecam zrobić rysunek do tego zadania. Ja zrobiłem screena i pozaznaczałem różne rzeczy:

Mamy policzyć tangens kąta XSY. Zaznaczyłem najpierw przekątną BD (czerwona linia, która jest też osią symetrii sześciana), potem X oraz Y, połączyłem X z B itd. i zaznaczyłem na niebiesko wysokości trójkątów (które są przekrojami) BDX oraz DBY (przydadzą się). Łącząc na fioletowo X z Y powstaje trójkąt XSY, tangens którego mamy obliczyć.

Ja myślę, że można to zadanie zrobić tak, że na końcowych etapach liczymy cos XSY, potem z jedynki trygonometrycznej sinus XSY, a potem zrobić z tego tangens. Ale przed tym mamy policzyć boki.

Ja bym zrobił tak, że od razu policzyłbym XS oraz SY (BD = AC = a√2  =>  AS = 1/2*a√2 i potem tw. Pitagorasa dla trójkątów ASX i SCY). Potem utworzyłbym na boku AE punkt Y' spełniający warunek, że AY'=1/5a i powstanie nam trójkąt XY'Y (XY'=AX-AY'). Z tego trójkąta liczymy XY (znowu Pitagoras).

Korzystamy z tw. cosinusów dla trójkąta XSY -> obliczamy cosinus.

Korzystamy z jedynki trygonometrycznej -> obliczamy sinus.

tga = sina/cosa

Jak masz jakieś pytania lub wątpliwości to śmiało pisz :)

Vlad, gdzie jest Narysowany y prim na obrazku?  I czy Kąt XSY nie będzie kątem prostym, bo tak wygląda na obrazku? I jeszcze mam pytanie czy XBY ten czarny trójkąt nie będzie prostokątny? Dzięki za pomoc, miłego dnia

Y' nie ma na obrazku, ale opisałem jak powstaje dany punkt. Tu jest obrazek z Y':

Odcinek |YY'| jest równoległy do |AC| i długość odcinka |AY'| jest równa długości |CY|.

Odnośnie kątu XSY: wątpie, że ten kąt jest kątem prostym, nie polecam sugerować się w takich kwestiach rysunkiem.

Tak samo z trójkątem XBY, wątpie, że jest prostokątny. Może jest, a może nie, należałoby zastosować tw. odwrotne do tw. Pitagorasa, aby sprawdzić czy ten trójkąt jest prostokątny.

Tobie również życzę miłego dnia :)