Fizyka zadanko
Zadanie 2.1
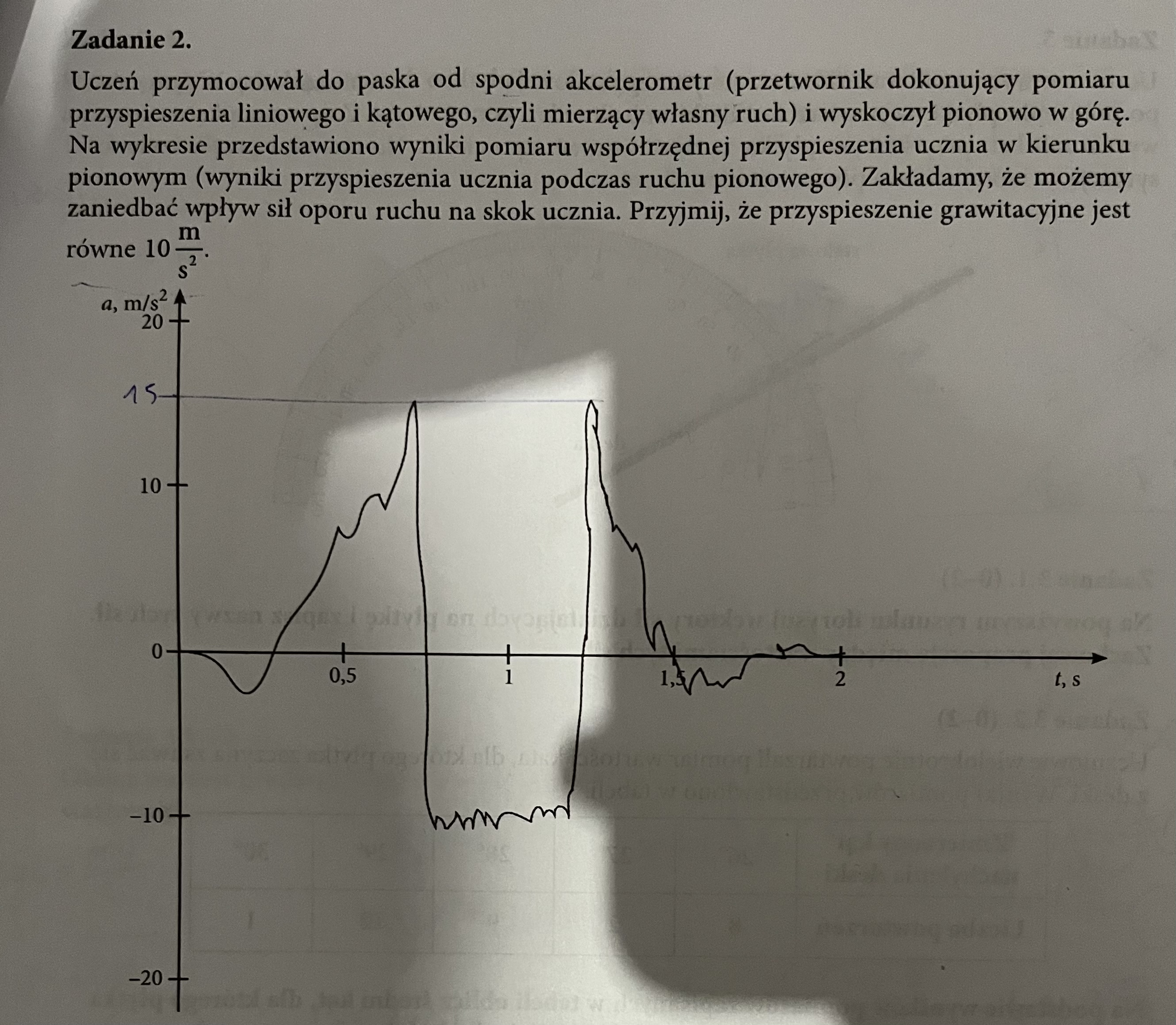
Na podstawie wykresu oszacuj, jak wysoko doskoczył ten uczeń
Zadanie 2.2. (0-2)
Masa ucznia była równa 76 kg. Oszacuj maksymalną wartość siłyz jaką uczeń naciskał podłogę podczas wyskoku
Będę wdzięczna za każde wskazówki :))
Fizyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Z wykresu należałoby wywnioskować, że w momencie gdy uczeń miał maksymalne przyspieszenie ok. 15 m/s^2 w górę, to wtedy nastąpiło jego oderwanie się od ziemi i potem przez ok. 0,5 s jego przyspieszenie było równe ok. 10 m/s^2 w dół (czyli było to przysp. grawitacyjne), czyli przez ok. 0,5 s znajdował się on w powietrzu. A zatem osiągnął on maksymalną wysokość po ok. 0,25 s. Potem przez ok. 0,25 s z tej maksymalnej wysokości spadał - był to spadek swobodny, więc wysokość, z której uczeń spadał można zapisać jako: h = gt^2/2 - stąd można oszacować tę maks. wysokość.
Co do drugiego podpunktu, to maks. nacisk na podłogę następował w momencie oderwania się od ziemi, bo wtedy przysp. ucznia było maksymalne. W tej zatem sytuacji na ucznia działały dwie siły - siła reakcji podłoża (równa co do wartości naciskowi ucznia na podłoże, więc to jest wielkość, ktorą chcemy policzyć) zwrócona pionowo w górę oraz jego ciężar zwrócony pionowo w dół. Wypadkowa tych sił sprawa, że przyspieszenie jakie ma w tym momencie uczeń wynosi ok. 15 m/s^2 (w górę). Wiedząc ponadto, że siła wypadkowa to oczywiście iloczyn m*a, możemy obliczyć jaka w tym momencie była wartość tej sił nacisku na podłoże (czyli to to samo co wartość siły reakcji podłoża).