suplement do zaj. 3 / zad. 2021.2.2
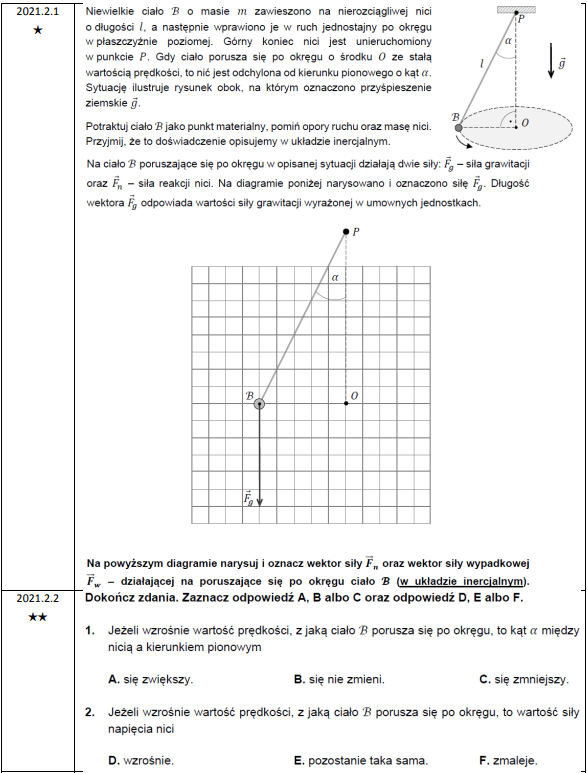
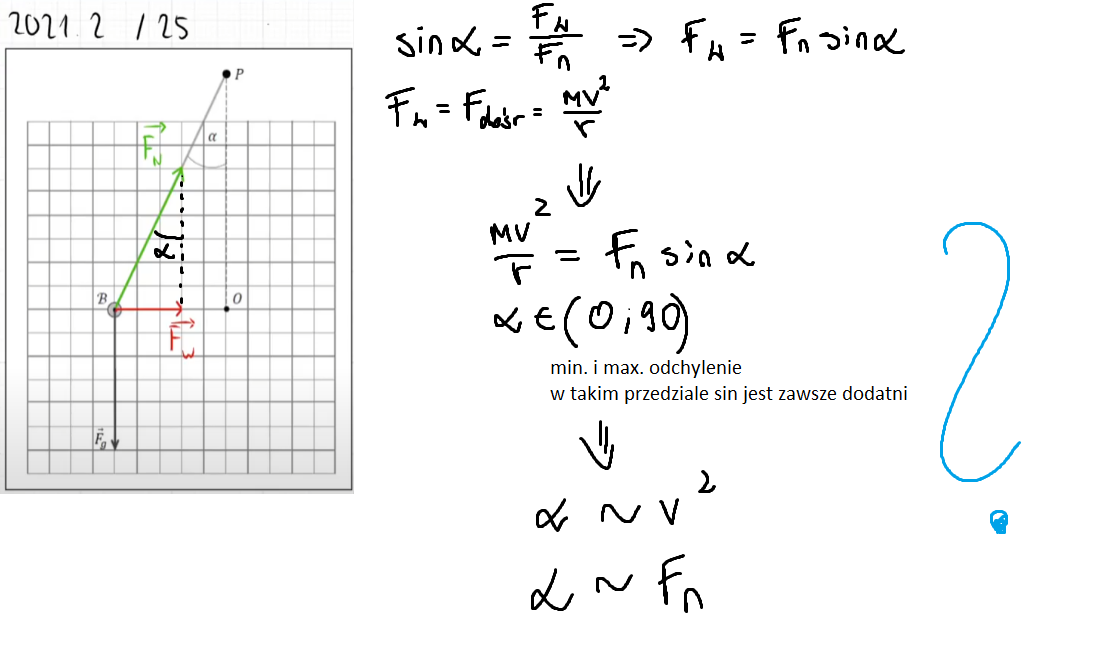
W suplemencie do lekcji nr 3 podpunkt 2. dla tego zadania został wyjaśniony jedynie na podstawie obserwacji z życia codziennego. Spróbowałem udowodnić to algebraicznie, prosiłbym o weryfikację i ewentualną poprawkę.
dynamika Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Rozumowanie matematyczne, które należy tu przeprowadzić jest dość trudne, dlatego nie decydowałem się go podawać na zajęciach. Równania, które zapisałeś są p[oprawne, ale niestety nie wynika z nich wniosek, który postawiłeś. Z treści wiemy bowiem tylko, że v rośnie (no i zakładamy oczywiście, że m jest stała). W związku z tym nie wiemy nawet czy lewa strona równania (mv^2/r) rośnie, czy też maleje, bo nie wiemy jak zmienia się r. Z tego też względu nie możemy powiedzieć nic konkretnego o prawej stronie równania.
Należałoby podejść do tego w następujący sposób (pewnie są inne wyprowadzenia, może nawet łatwiejsze): Zauważamy, że niezależnie od sytuacji Fn*cos(alfa) = mg (pionowa składowa Fn jest co do wartości równa sile ciężkości), a zatem m = Fn*cos(alfa)/g. Możemy to wrzucić do równania mv^2/r = Fn*sin(alfa) i wtedy Fn po obu stronach równania się skróci. Dostaniemy: v^2*cos(alfa)/gr = sin(alfa), stąd dostajemy: v^2 = gr*tg(alfa).
Teraz należałoby zauważyć, że sin(alfa) = r/l, gdzie l to długość nici (jest ona stała). A zatem r = l*sin(alfa) -> wstawiamy to do uzyskanego powyżej równania: v^2 = gl*sin(alfa)*tg(alfa). Teraz możemy zauważyć, że skoro lewa strona równania rośnie, to prawa też, a zatem iloczyn sin(alfa)*tg(alfa) rośnie. Zauważamy, że w przedziale od 0 do 90 stopni funkcje sin(alfa) oraz tg(alfa) są rosnące, a zatem jeśli ich wartość wzrosła, to kąt alfa również wzrósł. To byłoby wyprowadzenie odpowiedzi do pierwszego pytania ;)
Teraz wystarczy wrócić np. do równania Fn*cos(alfa) = mg. Prawa strona się nie zmienia, więc lewa również, ale wiemy już że alfa rośnie, a zatem cos(alfa) maleje, a zatem, żeby lewa strona pozostała stała, to Fn musi rosnąć.
Jak widać jest tu trochę zabawy, tak jak wspomniałem pewnie istnieje jakieś inne, być może łatwiejsze wyprowadzenie. Ale z tego względu dobrze jest mieć gdzieś w głowie własnie analogię z życia codziennego, bo wtedy zdecydowanie łatwiej i szybciej można sobie poradzić z takim zadankiem ;)