2021C.1.2
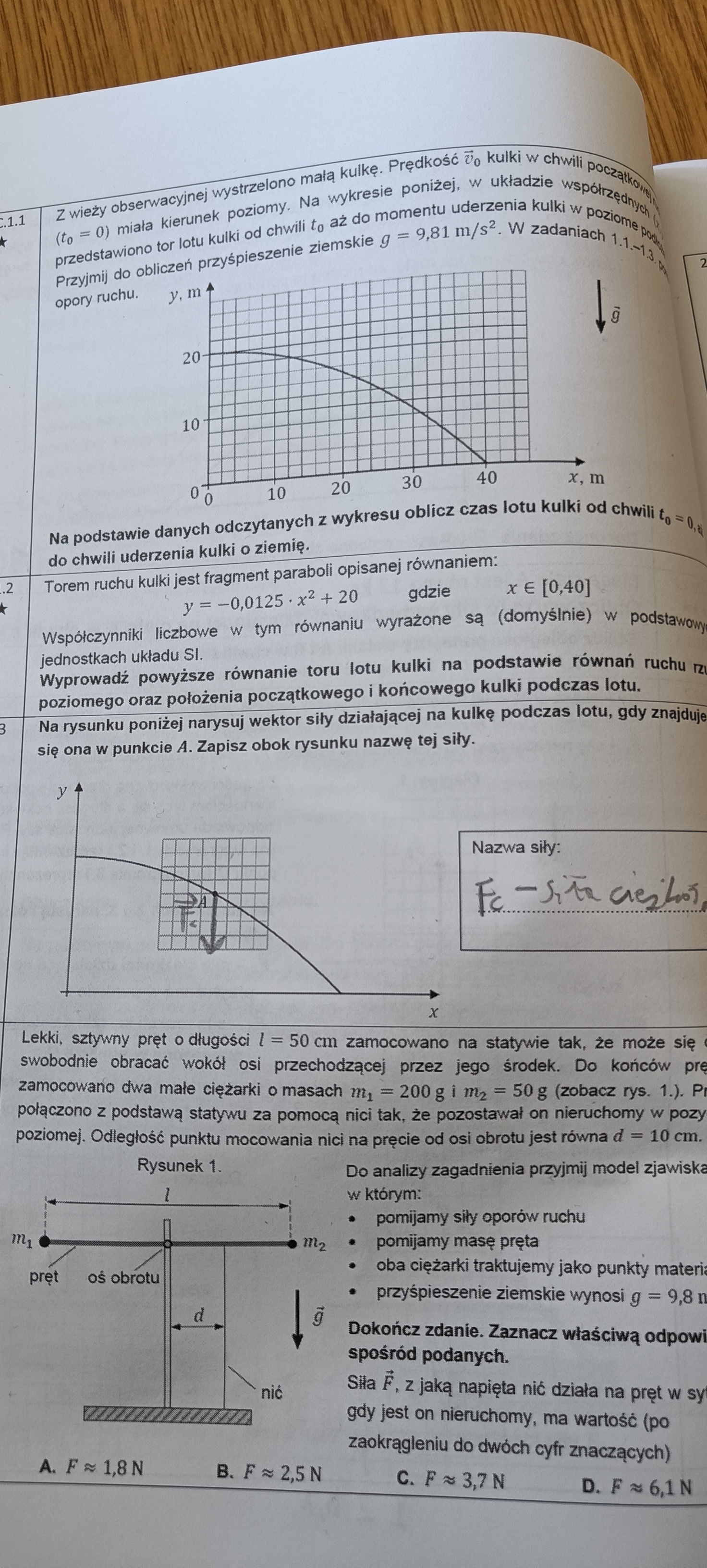
Jak zacząć robić to zadanie, myślałem żeby coś podstawić ale nie wiem co
Jedyne wzory które mi przychodzą do głowy żeby tu użyć to
x=v*t
y=(gt^2)/2
ale nie to jest rozwiązaniem zadania
Prosiłbym o jakieś naprowadzenie jak do tego podejść, zacząć a nie całe rozwiazanie
Fizyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
najdalej do czego udało mi się dojść to
y=h-gx^2/2*v^2
h=20m i zero pomysłu co z tym zrobić, Po 1,5h walczenia z tym zadaniem popatrzyłem sobie w kryteria oceniania na te zadanie i tam jest coś takiego ale nie wiem co z czego się bierze
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Naszym zadaniem jest ostatecznie wyznaczenie zależności y od x, więc musimy te dwie zmienne w jakiś sposób powiązać ze soba, stąd moja pierwsza podpowiedź, że skoro x = v*t, to t = x/v i można to wrzucić do równania na y i mamy powiązane ze sobą y i x, dostajemy wówczas to co sam już zapisałeś, czyli: y = h - gx^2/2*v^2. h znamy (jest równa 20 m), więc pozostaje nam tylko wyznaczenie v (jest to tak naprawdę vx - prędkość w kierunku poziomym, która jest stała w czasie trwania całego ruchu). No i tutaj można np. wykorzystać obliczenie, które było do zrobienia w podpunkcie pierwszym (zakładam, że go wykonałeś, skoro pytasz o podpunkt drugi ;)), bo tam przecież należało wyliczyć czas. Znając zatem czas i wykorzystując równanie v=x*t, możemy wstawić ten czas do tego równania (x też już mamy bo jest to 40 m dla t równego całkowitemu czasu ruchu) i zwyczajnie wyliczyć v. W rozwiązaniach to v podane jest jako xmax*pierw(g/2h), ale ten pierw(g/2h) to nic innego jak odwrotność czasu, który był właśnie do wyliczenia w pierwszym podpunkcie, więc tak na dobrą sprawę użyty jest tutaj wzór x = v*t => v = x/t.
Po wyliczeniu v wrzucamy ją do uzyskanego wzoru na y i dostajemy wzór, do którego mieliśmy dojść. Ważna uwaga - w tej sytuacji warto nie korzystać z zaokrągleń, tylko wykorzystując kalkulator naukowy jechać cały czas na zaokrąglonych wartościach, wtedy ten współczynnik przy x^2 wyjdzie nam faktycznie dokładnie równy -0,0125.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dobrze myślisz, tylko na sam początek należałoby wprowadzić jedną zmianę. y to wysokość na, której w danym momencie znajduje się kulka, więc równanie na y powinno wyglądać nieco inaczej (zauważmy, że oś y jest zwrócona w górę, a ciało przyspiesza w dół), mianowicie: y = 20 m - gt^2/2 (czyli niejako od początkowego położenia w pionie odejmujemy drogę przebytą w pionie, bo ciało porusza się przeciwnie do osi y). To raz, a dwa to zauważ, że np. z równania na x możesz wyciągnąć t i wrzucić do drugiego równania. W razie dalszych pytań pisz śmiało :)