kacper 775 wyśw. 14-10-2023 19:08

Zadanie maturalne 2007.7

Dany jest układ równań: 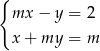{ mx − y = 2 x+ my = m .
Dla każdej wartości parametru 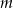m  wyznacz parę liczb 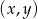(x,y) , która jest rozwiązaniem tego układu równań. Wyznacz najmniejszą wartość sumy 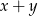x + y  dla m ∈ ⟨2,4⟩ .

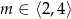Proszę o wyjaśnienie wszystkiego krok po kroku

Zadania maturalne matematyka Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Ania 15-10-2023 12:21

1. Na początku musisz rozwiązać ten układ równań-> wyliczyć z niego x i y (y powinien ci wyjść taki: y=(m^2-2)/(m^2+1), a x to: x=3m/(m^2+1)

2. Najmniejszą wartość sumy x + y wyliczysz po prostu poprzez dodanie tych dwóch wyrażeń.

3. Funkcję, która ci powstała w poprzednim podpunkcie, musisz z niej obliczyć pochodną (normalnie według wzoru z karty wzorów) (powinno ci wtedy powstać coś takiego: F'(x)=(-3m^2 + 6m + 3)/[(m^2+1)^2] )

4. Liczysz miejsca zerowe z licznika tej funkcji, rysujesz poglądowy rysunek, wyznaczasz ekstrema, lokalne maksimum (które jest najmniejszą wartością f(m) (oczywiście wszystko rozpatrujesz w przedziale m=<2,4>) i to tyle:)