Martyna 780 wyśw. 01-11-2023 16:25

zadania domowe

d) właściciel sklepu sprzedaje płyty z muzyką w cenie 130 zł, a kupuje z hurtowni w cenie 80 zł za sztukę. Miesięcznie sprzedaje 40 płyt. Sprzedawca zbadał rynek i okazało się, że każda obniżka ceny płyty o 1 zł spowoduje wzrost liczby sprzedanych płyt o 1 sztukę. Jaką cenę powinien ustalić sprzedawca za płytę, aby zysk był największy?

jak to zrobic 

matura matematyka Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Karolina 01-11-2023 21:05

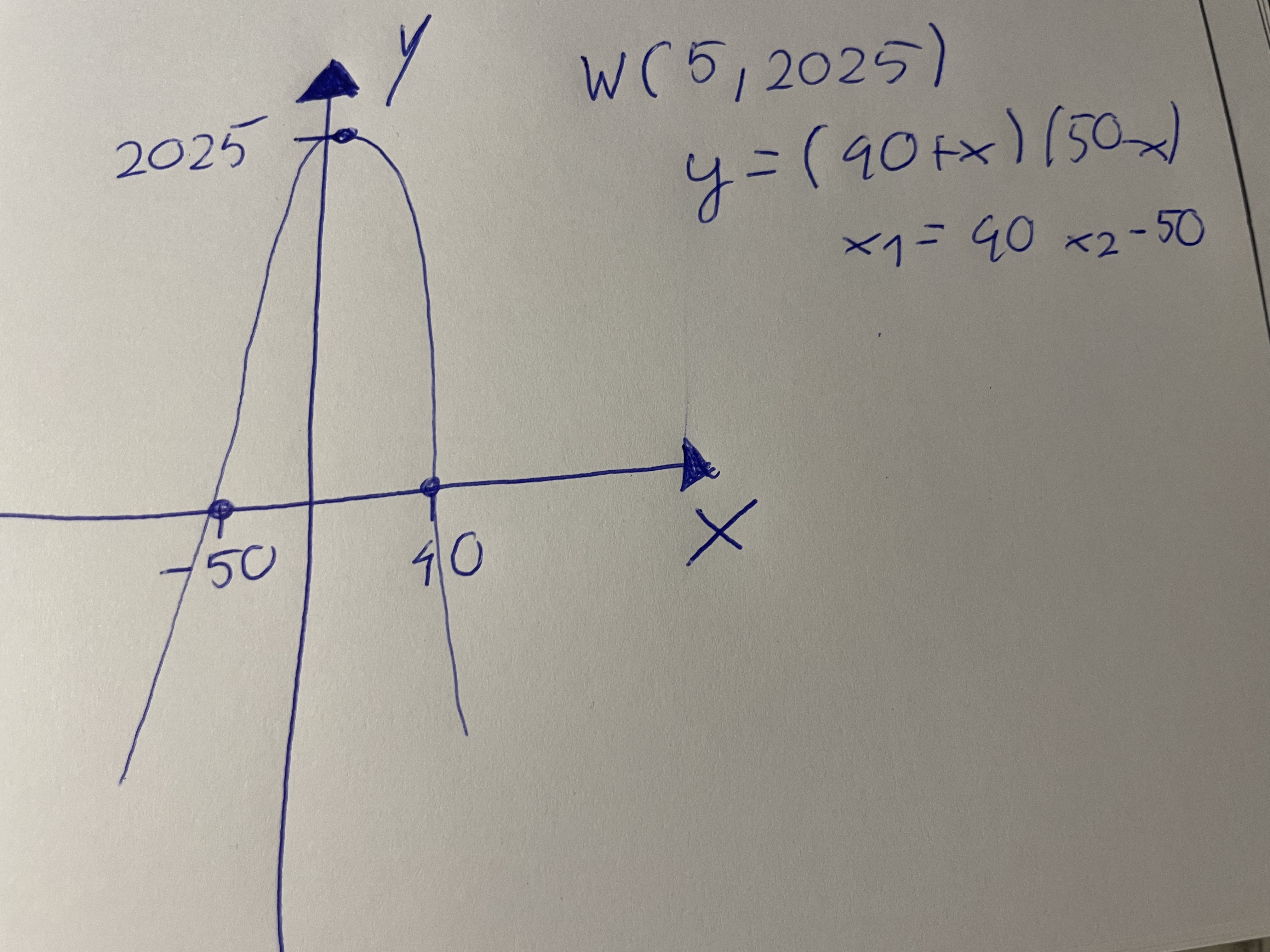
Witam :)

Przedstawiam moje rozwiązanie:

x- liczba kolejnych obniżek ceny jednej płyty

(50- x)- zysk ze sprzedaży jednej płyty

(40+ x)- liczba sprzedanych płyt


W kolejnym kroku zadania musimy sobie odpowiedzieć na pytanie jak wyglądała sytuacja zanim sprzedawca zaczął wprowadzać zmiany, więc obliczamy zysk:

40* 130zł= 5200zł- cena sprzedawcy

40* 80zł= 3200zł- cena hurtowa

130zł- 80zł= 50zł- zysk na jednej płycie

Zysk całościowy: 5200zł- 3200zł= 2000zł

y= ilość płyt* zysk z jednej płyty

y= (40 + x)(50 -x) =2000zł -40x +50x -x^2 = -x^2 +10x +2000

Po redukcji wyrazów wolnych powstał nam trójmian kwadratowy, jego współczynnik wskazuje nam na to, że parabola będzie skierowana w dół, zatem największą wartością jej będzie wierzchołek, a jeszcze dokładniej wartość q

W(p,q)

p= -b/ 2a

q= -trójmian kwadratowy/ 4a

a= -1 b= 10 c= 2000

trójmian kwadratowy: b^2 -4a*c

100 +4*2000 = 100 + 8000 =8100

trójmian kwadratowy= 8100

p= -10/-2

p=5

q= -8100/-4

q= 2025

W(5,2025)

Skoro p=x toooo:

(50- 5)- zysk ze sprzedaży jednej płyty= 45zł

(40+ 5)- liczba sprzedanych płyt= 45

Odpowiedź: Cena kurtki powinna wynosić 80zł+ 45zł= 125zł.







Karolina 01-11-2023 21:14

A tutaj interpretacja geometryczna:

Karolina 01-11-2023 21:15