Zadanie z treścią
Okrąg o równaniu x² + y² + 2y = 0 oraz parabola y = x² + a mają dokładnie jeden punkt wspólny dla: a=?
Rozwiązując zadanie graficznie poprzez narysowanie okręgu o środku w punkcie S(0;-1) oraz r= 1 można wywnioskować, że a=0 co jest poprawną odpowiedzią.
Jednak próbując rozwiązać to zadanie innym sposobem poprzez rozwiązanie układu równań wynik wychodzi inny. Jaki błąd popełniany jest przy drugim sposobie?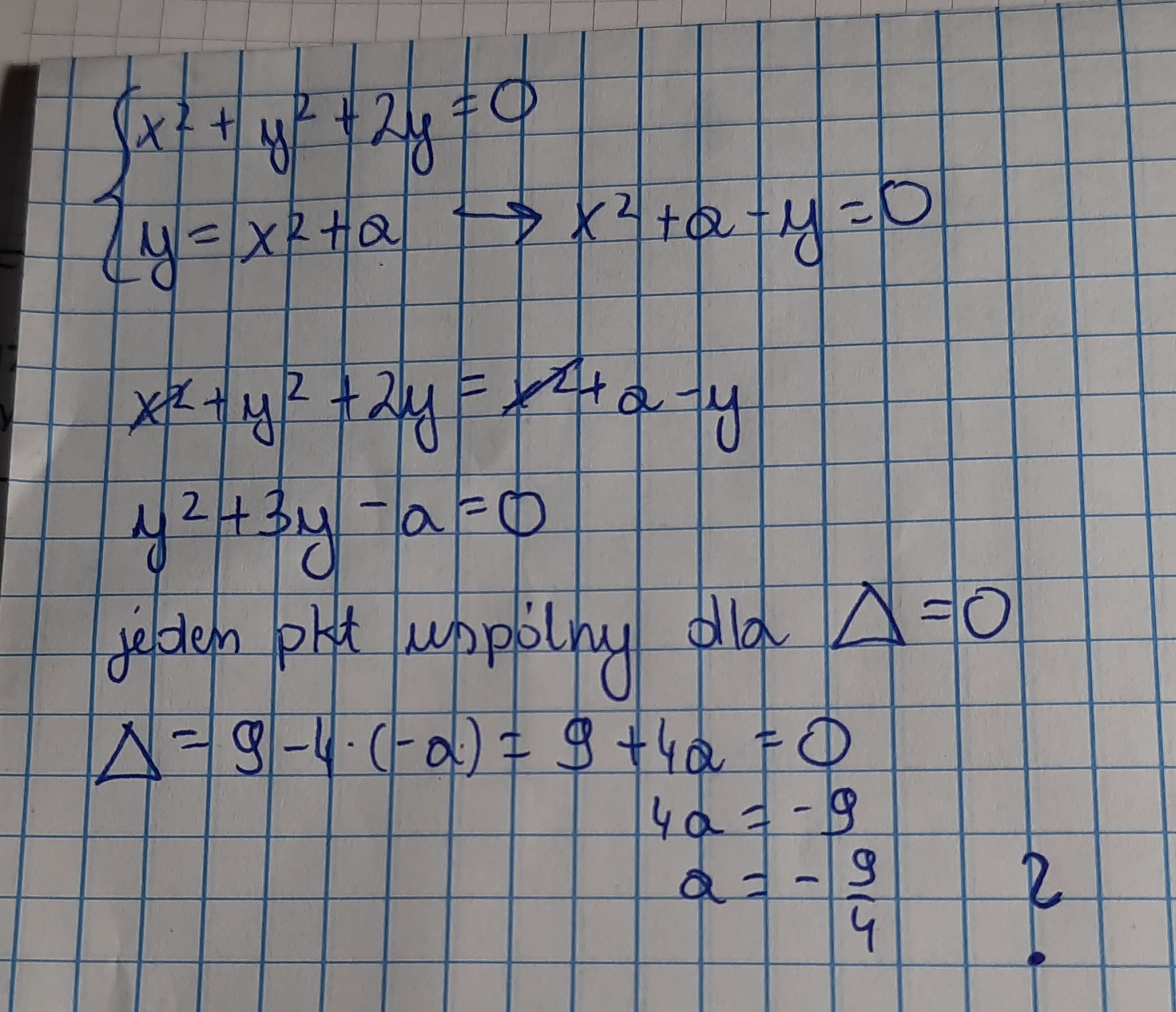
Matematyka geometria analityczna punkt wspólny Dodaj post do ulubionych Poproś o pomoc
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Problem w tym rozwiązaniu polega na tym, że dochodzi do utraty informacji. Spowodowane jest to tym, że z dwóch równań (paraboli i okręgu) uzyskujesz jedno, które nie jest bezpośrednio powiązane z pierwotnym układem równań.
Ogólnie mówiąc wyszło ci, że jest jedno rozwiązanie w zmiennej "y", ale to jedno rozwiązanie w "y" generuje dwa "x" co łącznie daje dwa rozwiązania :)
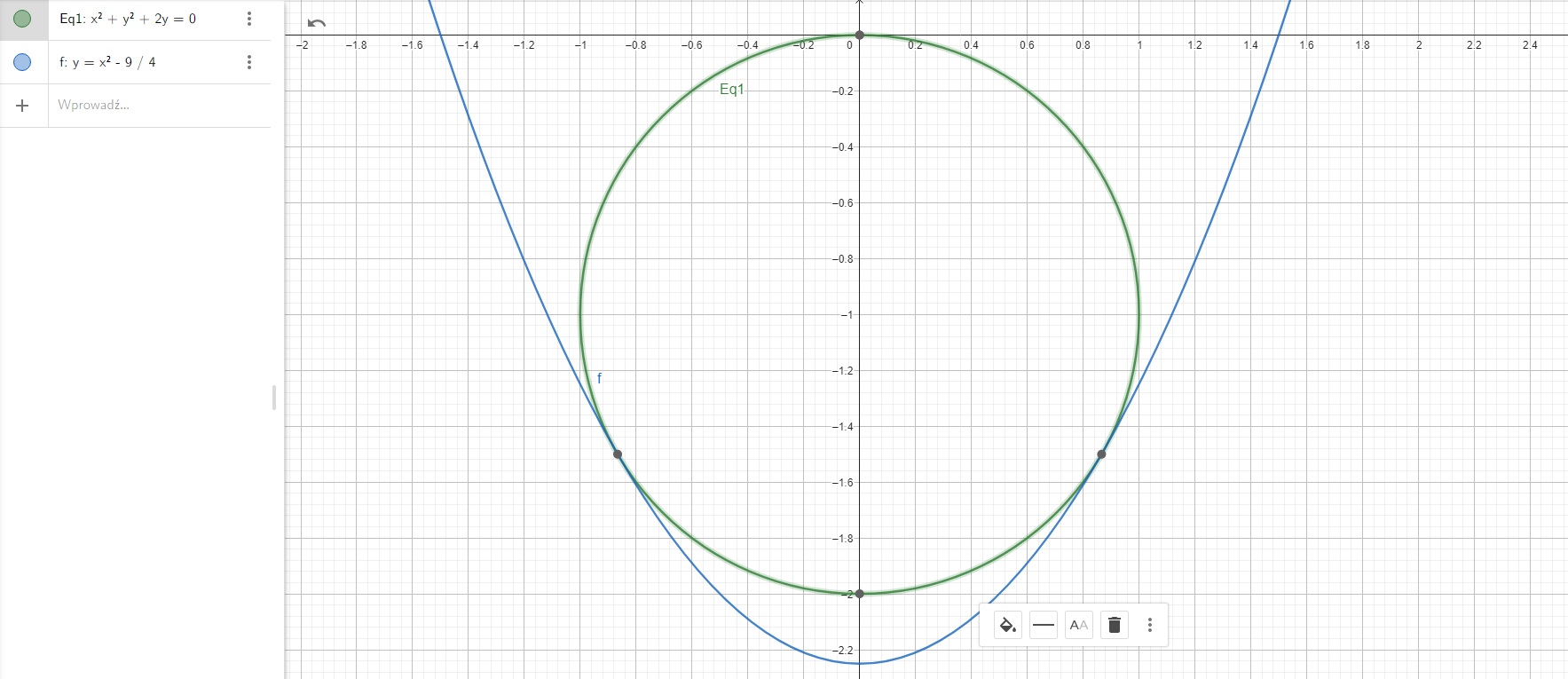
Spójrz na rozwiązanie które uzyskałaś:
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Problem w tym rozwiązaniu polega na tym, że dochodzi do utraty informacji. Spowodowane jest to tym, że z dwóch równań (paraboli i okręgu) uzyskujesz jedno, które nie jest bezpośrednio powiązane z pierwotnym układem równań.
Ogólnie mówiąc wyszło ci, że jest jedno rozwiązanie w zmiennej "y", ale to jedno rozwiązanie w "y" generuje dwa "x" co łącznie daje dwa rozwiązania :)
Spójrz na rozwiązanie które uzyskałaś: