Zad 1 Geometria analityczna 2
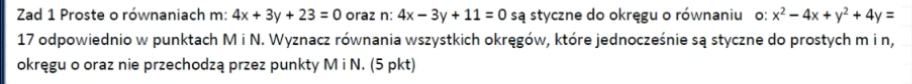
Zadanie próbowałem policzyć z podstawienia pod siebie wzorów na koło. Wiem, że nie jest to ani trochę optymalny sposób, do czego doszedłem dopiero w trakcie zadania, gdzie naszła mnie refleksja, że użycie wzoru na odległość może okazać się CIUT bardziej adekwatne. Postanowiłem jednak dokończyć to co zacząłem. Myślałem, że jeśli obliczę deltę z równania kwadratowego i jako parametr potraktuję zmienną “x” i przyrównam parametr do wartości przy której delta będzie równa 0, to wtedy koła te przecinać się będą tylko w jednym punkcie, bo będzie jedno miejsce zerowe, a więc koła te będą styczne. W wzorze jednego z nich, już uwzględniłem odległości od prostych licząc “r” jako zależność odległości środka okręgu od prostych. Mimo dużych liczb delta wyszła wymierna. Wynik natomiast jest dość absurdalny i ani trochę nie spełnia oczekiwań zadania. Ma ktoś pomysł na to, gdzie w moim wątpliwym rozumowaniu kryje się błąd? Zadanie już rozwiązałem, zależy mi w zasadzie tylko na usystematyzowaniu wiedzy.

Geometria analityczna Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli nie można tego zrobić w ten sposób?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Sprawdź jeszcze raz pod kątem błędu obliczeniowego to przejście: 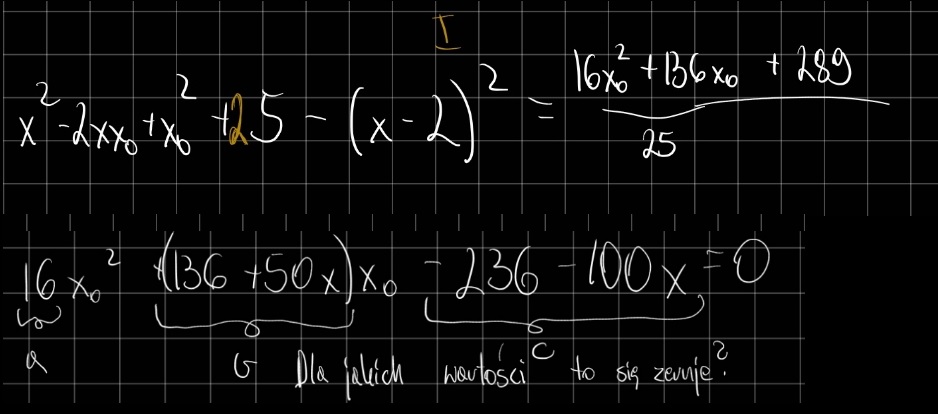
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Rzeczywiście, jest obliczeniówka. Dotarłem do oryginalnego równania koła : ) . Na maturze po tak zrobionym zadanku, po powrocie do domku trzeba by było napisać wiersz śmierci i wykonać seppuku. Dziękuję bardzo za pomoc, teraz udam się do jaskini i chwilę pomedytuję.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
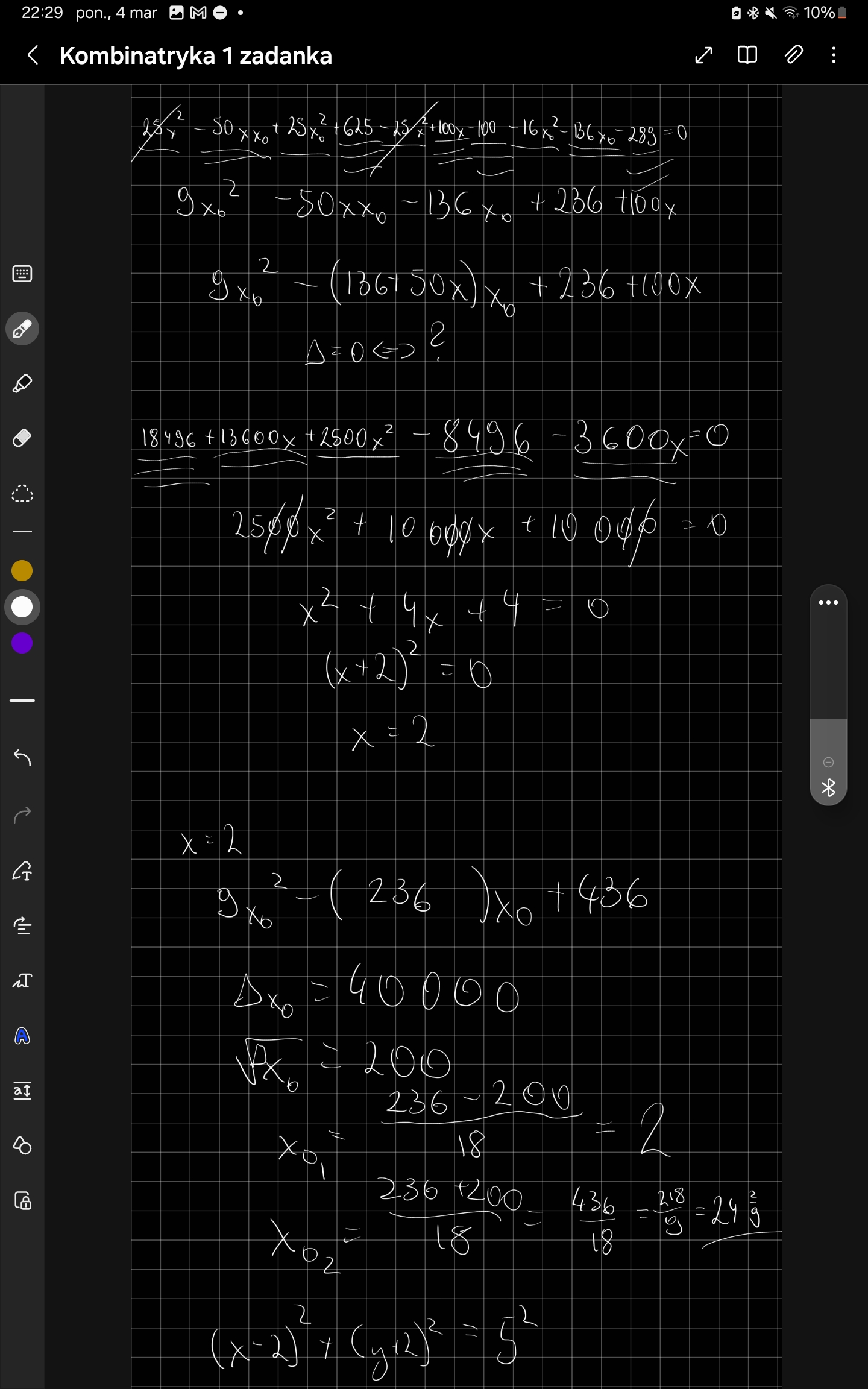
W jaki sposób obliczasz promień drugiego okręgu ? I w którym miejscu uwzględniasz styczność okręgu szukanego do obu prostych?