zadanie 10, arkusz 1, aksjomat
Zupełnie nie rozumiem, czemu w tym zadaniu używamy prawdopodobieństwa. Czy ktoś jest w stanie wytłumaczyć mi to rozwiązanie, bo pomimo wielu prób nie jestem w stanie sama tego zrozumieć.
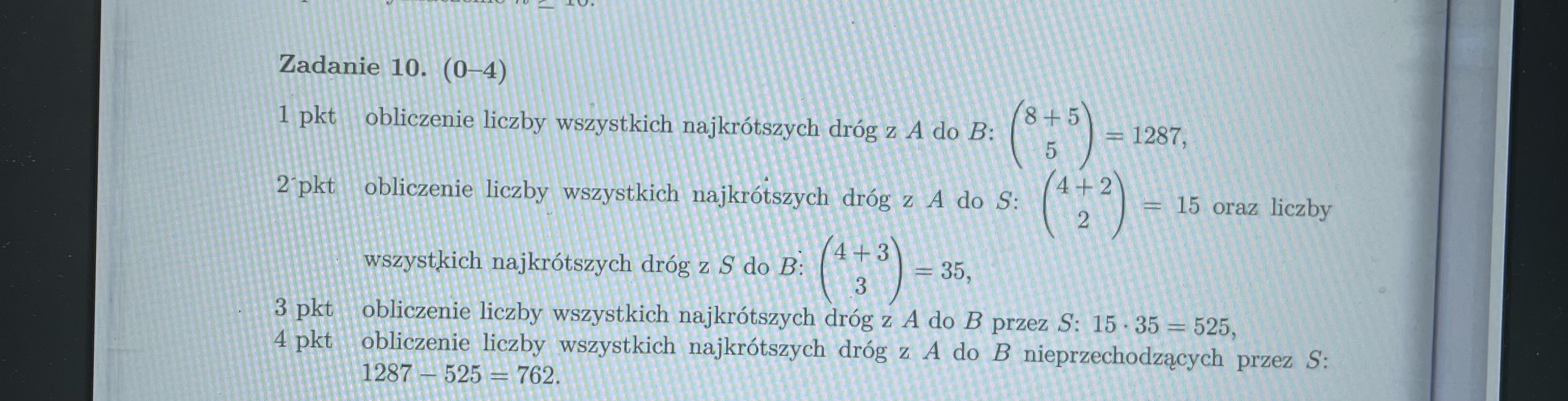
matematyka matura Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie używamy w tym zadaniu prawdopodobieństwa, a jedynie kombinacje, które pomagają nam obliczyć ilość możliwych tras.
Spójrz:
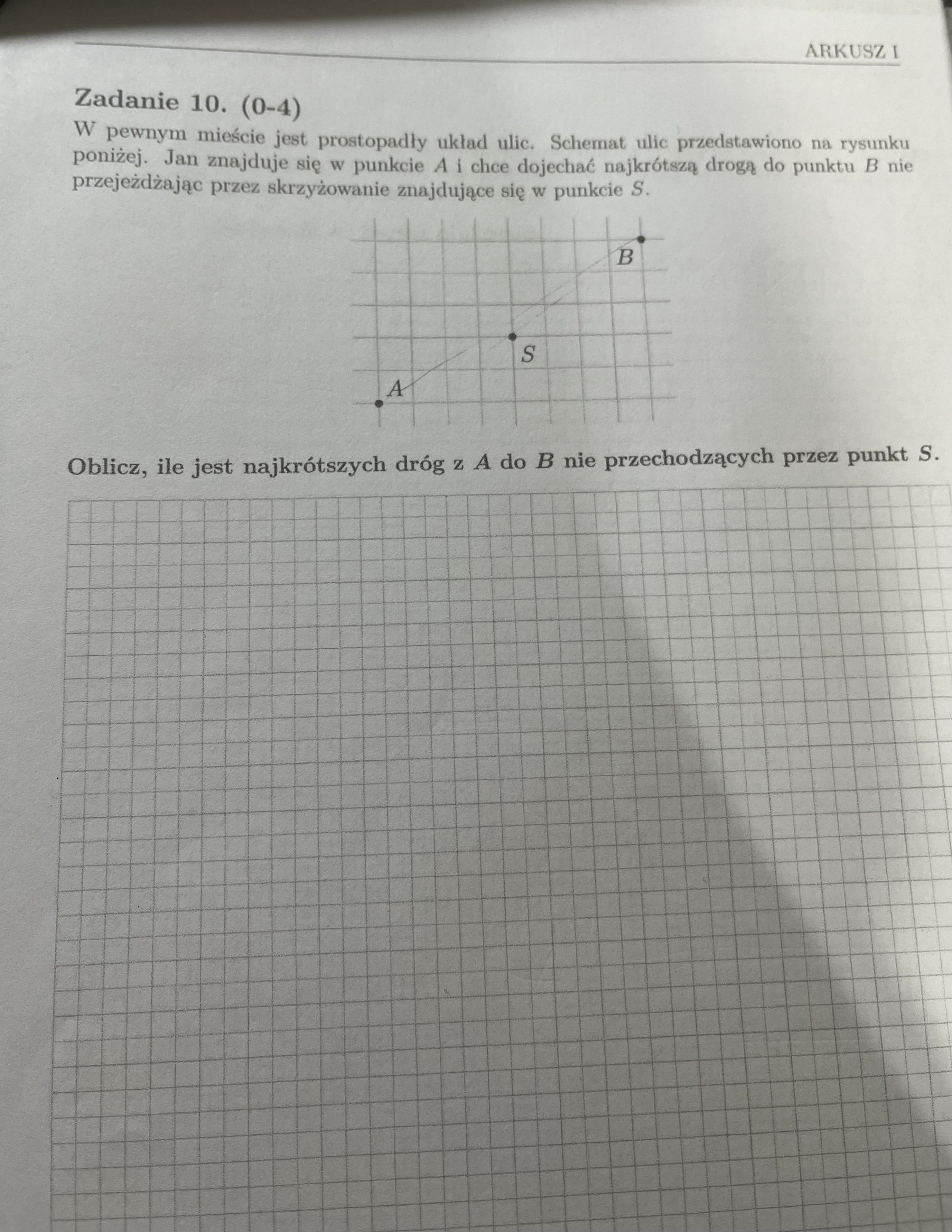
Żeby trasę móc nazwać najkrótszą musimy wykonać dokładnie 5 ruchów w górę i dokładnie 8 ruchów w prawo.
Każda trasa, w której dojdziemy do celu wykonując taką ilość ruchów możemy nazwać najkrótszą.
Oczywiście nie ma "jednej" najkrótszej trasy.
Możemy dojść do celu tak jak narysowano na rysunku powyżej czyli idąc 5 razy w górę a następnie 8 razy w prawo, ale równie dobrze nasza trasa może wyglądać następująco:
Problem możemy sobie zwizualizować w ten sposób:
mamy 5 dostępnych ruchów w górę G, G, G, G, G oraz 8 dostępnych ruchów w prawo P, P, P, P, P, P, P, P.
Teraz musimy zastanowić się na ile sposobów możemy utworzyć 13 elementowy ciąg, który będzie reprezentował naszą trasę.
Mamy zatem do obsadzenia 13 miejsc:
_ _ _ _ _ _ _ _ _ _ _ _ _
Obliczmy zatem na ile sposobów możemy utworzyć taki ciąg:
wybieramy 5 miejsc na ruchów "G" na: (13 po 5) sposobów, pozostałe miejsca zajmują ruchy w prawo "P", na jeden sposób (po prostu zajmują pozostałe miejsca). Zatem ilość najkrótszych tras, które mamy wynosi tak jak w kryteriach (13 po 5) 1287 sposobów.
Dodatkowo w zadaniu wymagają od nas abyśmy ominęli punkt S, zatem tak jak w kryteriach sprawdzamy na ile sposobów możemy dojść do celu przechodząc przez punkt "S" tak aby trasa była najkrótsza.
Zatem do punktu S najkrótsza trasa to ciąg składający się z 4 ruchów w prawo oraz 2 ruchów w górę.
Następnie najkrótsza trasa z punktu S do punktu B składa się z 4 ruchów w prawo i trzech w górę.
Analogicznie wykorzystując kombinacje obliczamy ilość sposobów tak jak w kryteriach.
W razie jakichkolwiek problemów proszę śmiało pisać :)