zadanie 8 praca domowa nr 24. matematyka rozszerzona

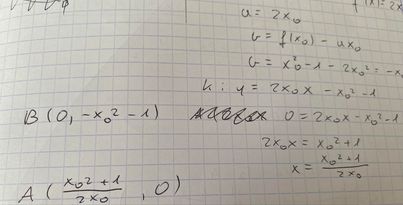 nie rozumiem dlaczego w miejscu zerowym wokol x0 w mianowniku jest wb ktos wytlumaczy?
nie rozumiem dlaczego w miejscu zerowym wokol x0 w mianowniku jest wb ktos wytlumaczy?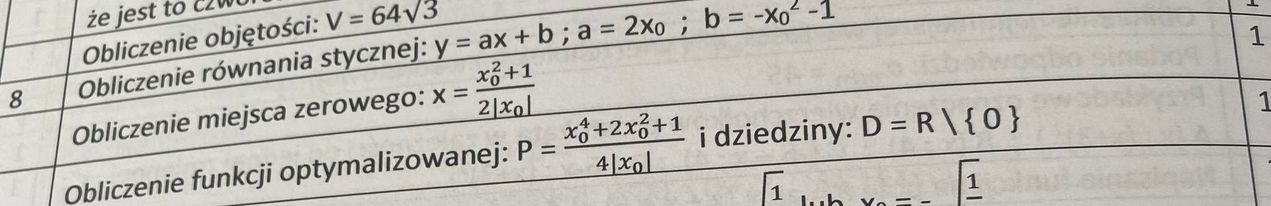
matematyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
nie wiem czy to co teraz pisze dziala jak odpowiedz na komentarz pod spodem xd ale chodzilo mi o wb w miejscu zerowym stycznej, rozumiem dlaczego we wzorze funkcji jest wb ale w miejscu zerowym stycznej?
"obliczenie miejsca zerowego x=x0^2+1/2|x0|"
bo z tego co rozumiem miejsce zerowe nie musi dodatnie samo w sobie dopoki nie traktuje go jako dlugosc odcinka
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Miejsce zerowe nie musi być dodatnie, ale już odcinek musi dlatego dajemy wartość wb.
x=|x0^2+1/2x0|, jeżeli x0^2 + 1 > 0 to w liczniku możemy opuścić wb.
Mamy teraz x=x0^2+1/|2x0|, tutaj np |2x0| = 2|x0|.
Dlatego miejsce zerowe to x=x0^2+1/2|x0|.
Tobie pewnie chodzi o to czemu miejsce zerowe ma wb jak to odcinek ma być dodatni, a nie miejsce zerowe?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przyprostokątne trójkąta muszą być dodatnie, ponieważ nie możemy mieć odcinków ujemnych.
P = ef/2, gdzie: e - przyprostokątna trójkąta należąca do osi ox, f - druga przyprostokątna należąca do osi oy.
g(x) - wzór stycznej
Więc przyprostokątne mają długości:
e - miejsce zerowe stycznej, czyli e = |x0^2+1/2x0|
f = |-x0^2 -1|, czyli współczynnik b stycznej
Obydwa oczywiście pod wb.
Po podstawieniu do wzoru na pole w liczniku wb możemy opuścić bo |-(x0^2 + 1)^2| = (x0^2 + 1)^2, gdzie (x0^2 + 1)^2 >=0 , lecz w mianowniku tej wb już nie możemy opuścić. Dlatego ona pozostaje.