Przy.N.11 strona 51
Egzamin składa się z 15 zadań zamkniętych. Do każdego zadania podano cztery odpowiedz, iz których tylko jedna okazuje się poprawna. Zdający zalicza egzamin, jeśli udzieli poprawnych odpowiedzi w co najmniej 11 zadaniach. Pewien student przystąpił nieprzygotowany do egzaminu i w każdym zadaniu wybierał losowo odpowiedź. Przyjmij, że w każdym zadaniu wybór każdej z odpowiedzi przez studenta jest równo prawdopodobny. Oblicz prawdopodobieństwo zdarzenia, że ten student zaliczył egzamin
Witam, natknąlem się na to zadanie i nie sprawiało mi problemów do momentu kiedy musiałem obliczyć finalny wynik wynoszący 123841/4^15, po w klepaniu w kalkulator, ale nie prosty (O ile się nie pomyliłem). Pytanie moje więc dotyczy sposobu zapisania wyniku, gdyż nie wyobrażam sobie liczyć np. 4^15, czy nawet 4^11 w warunkach maturalnych, a potem jeszcze wykonywać działania na ułamkach z takimi liczbami. Czy wystarczy podać ułamek taki jak pisałem powyżej a może wystarczy zostawić ten wynik w postaci gdzie sumuje wszystkie prawdopodobieństwa? 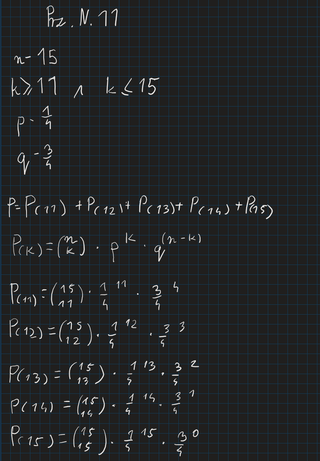
Matematyka kombinatoryka 4^15 8D Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Na maturze:
1/ zawsze będzie doprecyzowane w jakiej postaci zostawić wynik
2/ kalkulator prosty zawsze da radę obliczyć to co trzeba
3/ unikną kontrowersji i "dziwnych wyników"