Angel 47 wyśw. 14-03-2024 22:19

Zmiana znaku wynikającą z monotoniczności logarytmu


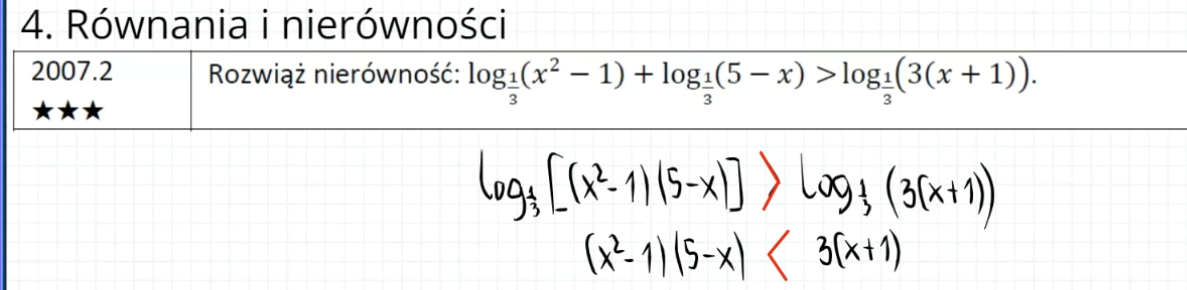
Pan tłumaczył na lekcji o logarytmach czemu kierunek znaku się zmienia i że wynika to z monotoniczności logarytmów, jednak ja nadal nie do końca to rozumiem:)
Byłyby ktoś w stanie wytłumaczyć mi to?

logarytmy Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 16-03-2024 14:11

Żeby to zrozumieć musimy spojrzeć na wykresy funkcji logarytmicznej.

1. Logarytm którego podstawa jest z przedziału (0, 1) jest "funkcją" malejącą, z kolei logarytm którego podstawa jest z przedziału > 1 jest "funkcją" rosnącą:

Zatem jeżeli mamy mamy do rozwiązania nierówność, w której z obu stron mamy logarytm o podstawie mniejszej od 1 musimy się chwilę zastanowić.

Gdy mamy log_c(A) > log_c(B), gdzie A, B - argumenty oraz c- podstawa mniejsza od 1.

Dla jakich argumentów  logarytm log_c(A) będzie większy od logarytmu log_c(B). Skoro obie funkcje są malejące to naturalne, że log_c(A) będzie większy wtedy gdy jego argumenty będą mniejsze od argumentów log_c(B). 

Spójrz jeszcze na rysunek: