arkusz 2 zadanie 11/19s

---

Mam problem z dziedzina, mozliwe, ze wynika on z obliczen :
1) h = 2r = 8cm
2) z Tw. Pit : AD = CB = sqrt(64 + y^2)
3) warunek na okrag wpisany w czworokat : 64 + y^2 = x^2 + 2xy + y^2 --> y = (64 - x^2)/2x

Po optymalizacji wyszlo mi, ze pochodna zeruje sie dla x = 8 i x = -8, lecz dziedzina nie zgadza sie juz z odp, bo wydaje mi sie, ze x > 0 i y > 0, wiec x nalezy (0,8) i z dziedziny wynika, ze nie ma argumentu, dla ktorego funkcja ma wartosc minimalna w tym przedziale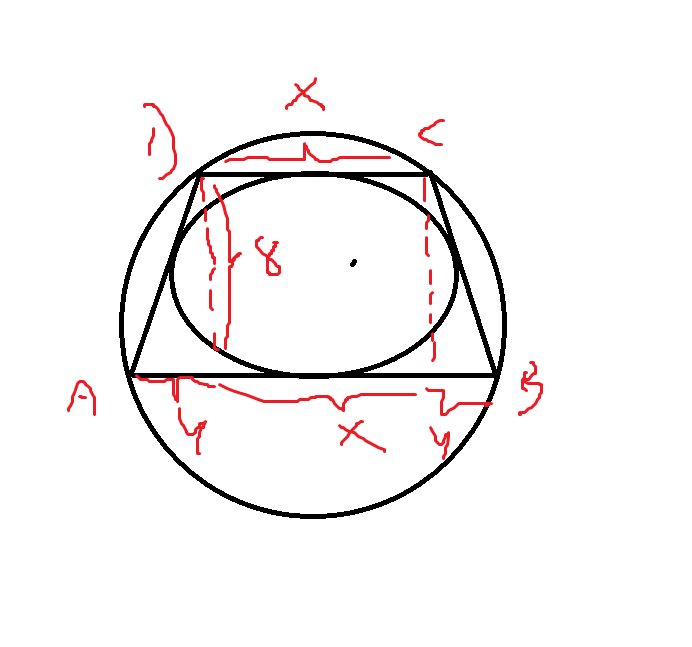


Z czego wynika, ze mozna wlaczyc ta 8, przeciez wtedy y = 0, a odc musi byc dodatni 

---

dziedzina Dodaj post do ulubionych Poproś o pomoc