zad 7 arkusz 11
wyznacz równanie dwusiecznej kąta ostrego, stworzonego przez proste x+Y+7=0 i x-7y-3=0
Podałby ktoś rozwiązanie tego zadania tą metodą z użyciem tangensa?? Byłabym wdzięczna
arkusz Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Spróbuj podejść do tego w ten sposób:
Oznacz szukaną prostą jako: y = ax + b
Wykorzystaj wzór:
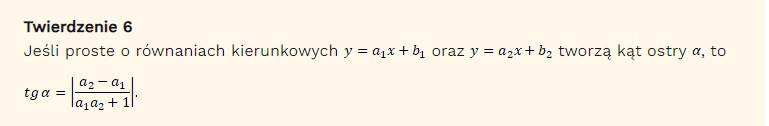
W ten sposób obliczysz tangens kąta ostrego między prostymi.
Mając tangens kąta między prostymi możesz wyliczyć tangens(alfa/2).
Teraz ponownie skorzystaj z wyżej wymienionego wzoru, aby znaleźć współczynnik "a" szukanej prostej (znając również tangens(alfa/2).
Pozostało wyznaczyć "b", wykorzystując fakt, że prosta przechodzi przez punkt przecięcia się danych w zadaniu prostych.
W razie problemów proszę śmiało pisać :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@jarosinski czy ma pan moze to rozwiazane? mi ciagle wychodzi zle ta metoda mianowicie sama polowa kata jest rozna od tego, ktora wychodzi obliczajac pierwsza metoda (odleglosc pkt. taka sama) bo tg alfa miedzy tymi prostymi z zadania jest rowny 4/3 wiec dwusieczna daje kat 2/3. Ze sposobu pierwszego tego zadania tg alfa wychodzi 1/2 albo 2.
Proboawlem mimo wszystko brnac w to dalej ale b (dwueisecznej) wyszlo -12/5 albo -30 i nic z tego
dodatkowo chce zaznaczyc ze obydwa te katy wytwarzane miedzy tymi prostymi sa w takim razie ostre, jeden mniej ostry drugi bardziej.
Skad te rozbieznosci?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
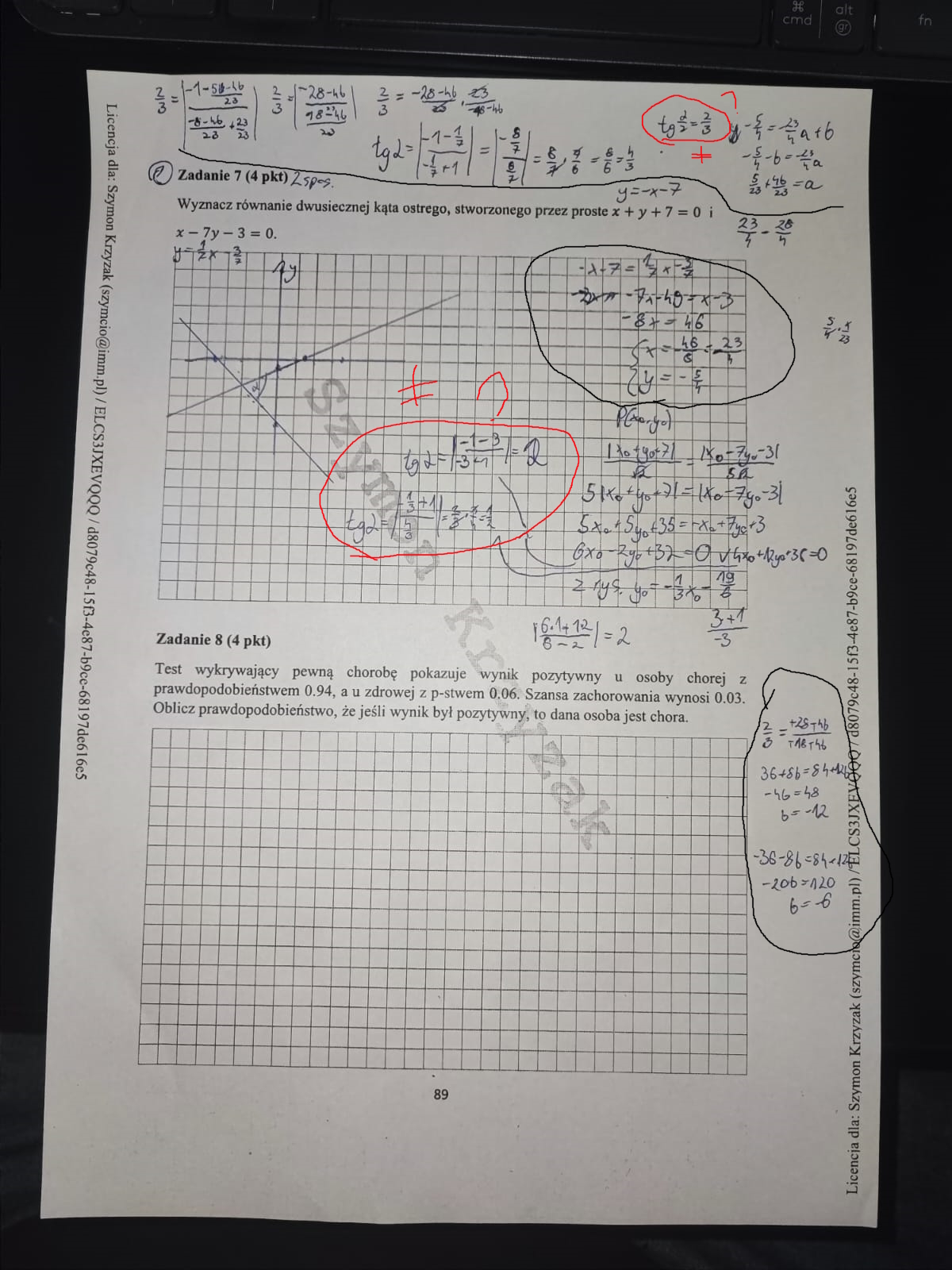tu jeszcze oznaczylem dodatkowo elementy ktore mnie zastanawiaja, przeciez te katy powinny wyjsc takie same co tu poszlo nie tak
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale tg (alfa/2) to nie jest tg(alfa) / 2. Musisz skorzystać z wzoru na tangens podwojonego kąta.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Spróbuj podejść do tego w ten sposób:
Oznacz szukaną prostą jako: y = ax + b
Wykorzystaj wzór:
W ten sposób obliczysz tangens kąta ostrego między prostymi.
Mając tangens kąta między prostymi możesz wyliczyć tangens(alfa/2).
Teraz ponownie skorzystaj z wyżej wymienionego wzoru, aby znaleźć współczynnik "a" szukanej prostej (znając również tangens(alfa/2).
Pozostało wyznaczyć "b", wykorzystując fakt, że prosta przechodzi przez punkt przecięcia się danych w zadaniu prostych.
W razie problemów proszę śmiało pisać :)