Kombinatoryka

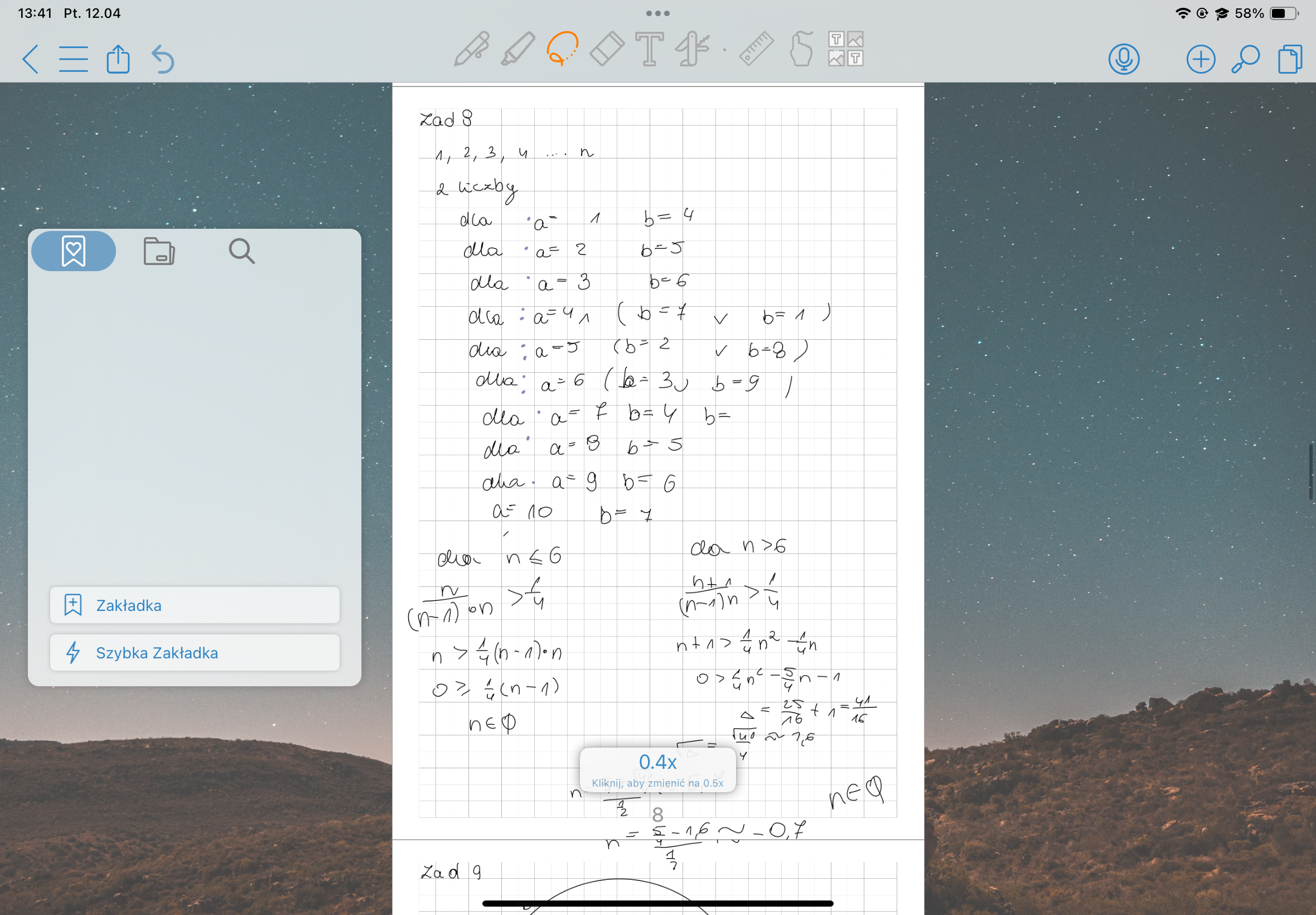
Zamysł raczej dobry i dobrze jest wyznaczona liczebność zbioru możliwych zdarzeń ( (n-1)*n ) można zwrócić jednak uwagę na dwie rzeczy:

1) Być może coś pomijam, ale podział na te dwa przypadki: n ≤ 6 oraz n > 6 wygląda na niekorzystny pomysł.
Na przykład dla n = 5 mamy 4 pary
dla n = 6 mamy 6 par
a dla n = 7 mamy 8 par
Formuła się nie zmienia (wzór jest taki sam dla n = 5, n = 6 czy n = 7)

2) Nawet gdyby tak było, czy na pewno dla n = 5 mamy n par jak w powyższym rozwiązaniu? Czy na pewno dla n = 8 mamy n + 1 par?

Chyba łatwiej by to było rozpisać właśnie licząc liczbę par dla kilku przykładowych n (i znaleźć tę formułę, jak w kryteriach).

Fajne tło, tak przy okazji ; )