Informator maturalny 2022/2023 zad.1.2
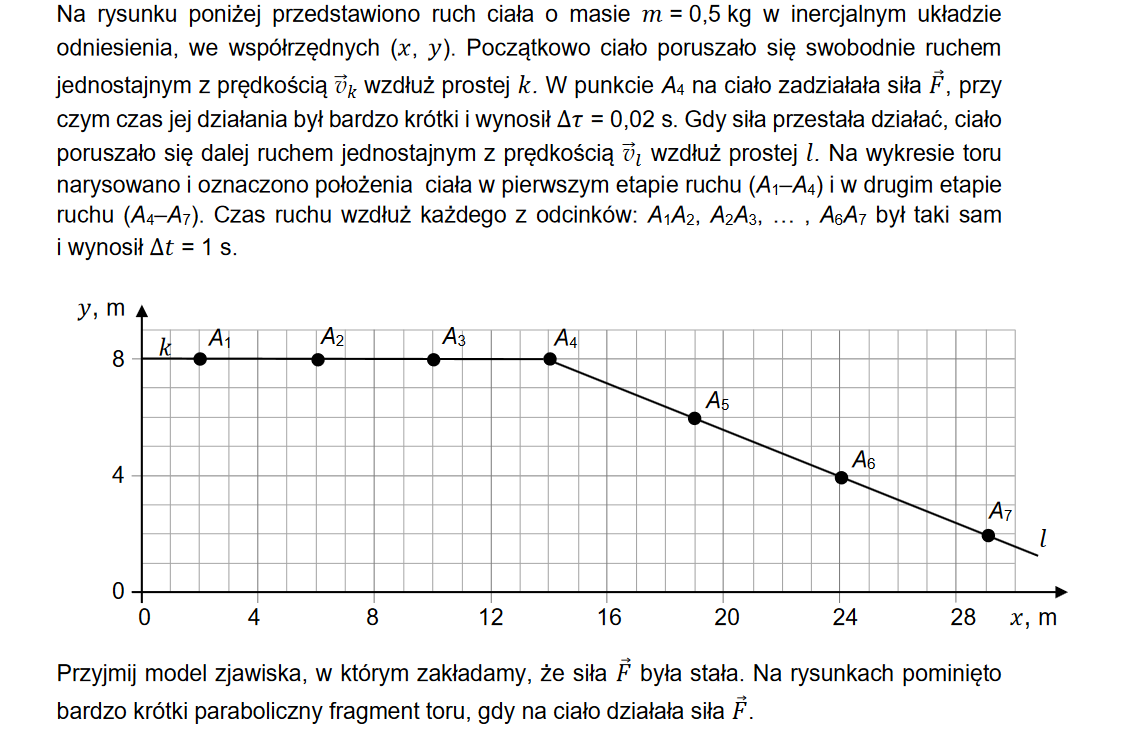

Dzień dobry, próbowałam rozwiązać to zadanie i myślałam że jest dobrze, ale w odpowiedziach jest, że F=56N. Proszę o pomoc i wskazanie, gdzie jest błąd

fizyka dynamika informator siła Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chodzi o to, że druga zasada dynamiki, którą tu używasz z siłą i zmianą pędu to równanie wektorowe. Czyli wygląda ono tak naprawdę tak:
$$ \overrightarrow{F} = \frac{\overrightarrow{\Delta p}}{\Delta t} $$
Oznacza to, że najpierw trzeba określić jaki jest wektor zmiany pędu delta p, jako: deltap = p2 - p1, przy czym to równanie jest również równaniem wektorowym! Czyli najpierw wykorzystując rysunek należy narysować sobie wektor p1, wektor p2, odjąć od p2 wektor p1 (graficznie odejmujemy wektory) i wyjdzie nam jakiś wektor deltap. Jego długość będziemy mogli wyrazić poprzez długośc wektora p1 (albo wektora p2), a długości obu tych wektorów jesteśmy w stanie policzyć, bo będą to po prostu wartości wektorów p1 i p2 (czyli odpowiednio mv1 lub mv2). Stąd obliczymy długość wektora deltap, czyli będziemy mieli jego wartość. I dopiero tak obliczoną wartość deltap będzie można wrzucic do wartościowego równania F = deltap/deltat.
Czyli skrótowo rzecz ujmując, wartość deltap nie jest równa różnicy wartości p2 i p1, trzeba najpierw zrobić odejmowanie wektorowe i dopiero potem na tej podstawie wyznaczyć wartość wektora deltap. W razie dalszych pytań pytaj oczywiście śmiało. Swoją drogą to dokładnie zadanie robiliśmy również na naszych zajęciach nr 4 - jest to na nagraniu, warto tam z pewnością zerknąć, bo jest tam opisany przeze mnie proces w całości przedstawiony :)