DK 203 wyśw.
28-04-2024 17:58
zad 25 arkusz 1 str 12
Kąt alfa jest ostry oraz sin alfa= 2\7. Oblicz tg alfa-sin alfa\ tg alfa+ sin alfa
Proszę o pomoc w rozwiązaniu zadania. Z góry dziękuję za jakąś podpowiedź lub rozwiązanie.
Matematyka matura arkusze maturalne podstawa Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski
28-04-2024 19:29
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jarosinski
28-04-2024 19:31
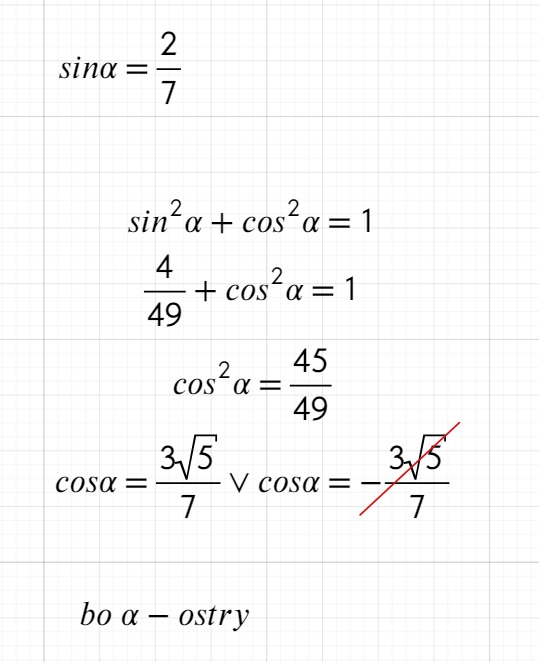
Podpowiedź:
- Wykorzystaj fakt, że kąt alfa jest ostry oraz, że sin(alfa)=2/7
- Wykorzystaj jedynkę trygonometryczną tzn: sin^2(alfa)*cos^2(alfa)= 1
Z niej wyliczysz cosinus -> wyjdą ci dwa rozwiązania natomiast wiedząc, że kąt alfa jest ostry możesz odrzucić ujemne rozwiązanie cosinusa.
Pozostało tylko podstawić odpowiedni sin(alfa) oraz cos(alfa) do wzoru na tangensa i wyliczyć wyrażenie.
Jeżeli w dalszym ciągu masz problem, wstaw proszę poprawnie sformatowane wyrażenie (np. w formie zdjęcia).