Drgania, wahadło matematyczne

Zadanie 11.3
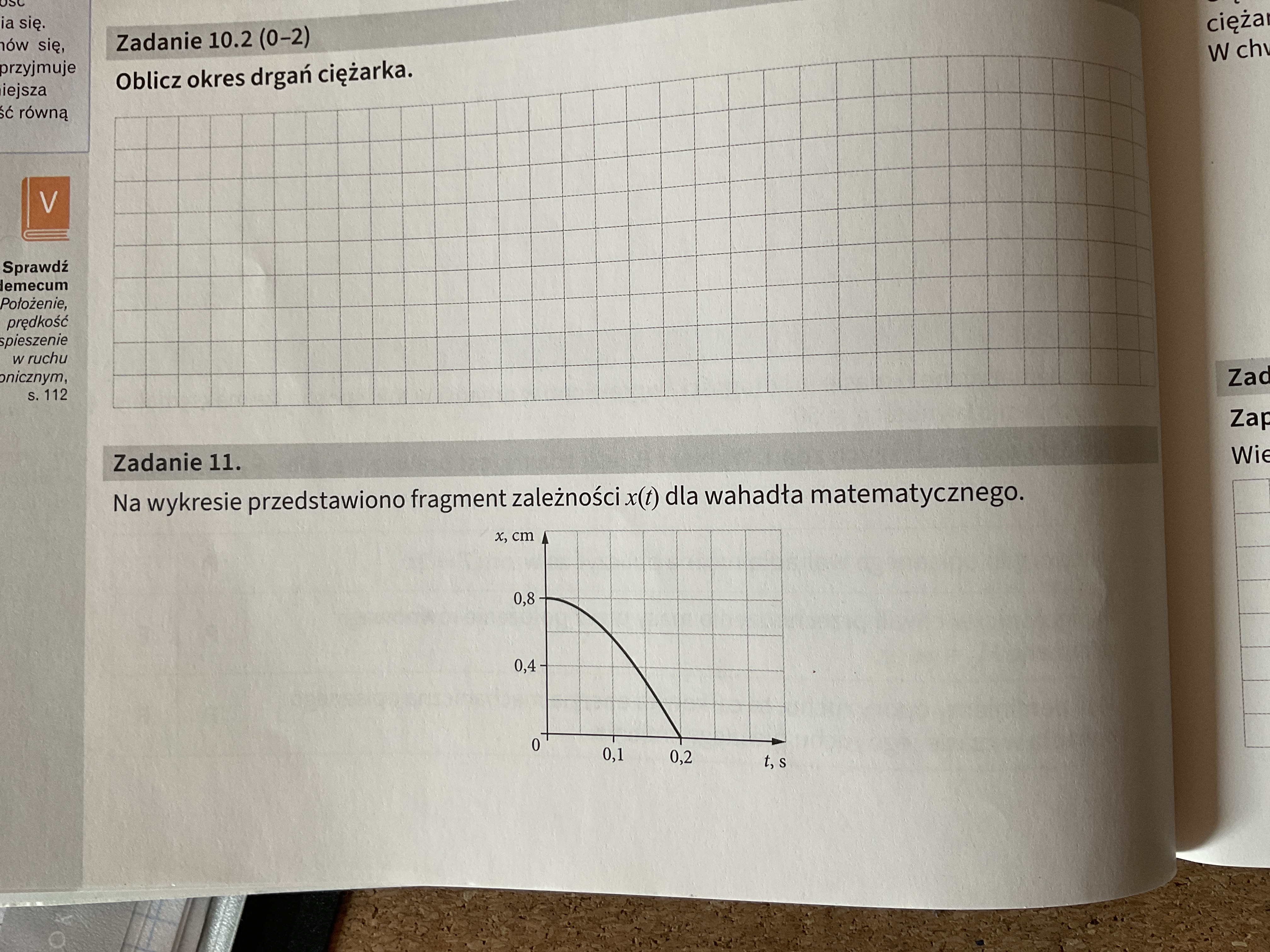
W odpowiedziach było rozw. uzasadniające, że ze wzoru na okres dla małych kątów wynika, że nie jest on zależny od amplitudy, więc wahadło osiągnie położenie równowagi po tym samym czasie, czyli 0,2 sekundy.
Jednak czegoś nie rozumiem: ja zrozumiałam to zadanie tak, że zmieniamy tylko położenie początkowe, ale amplituda jest dalej 0,8 cm. Wtedy ten ruch byłby przesunięty o jakąś fazę? Czy to w ogóle można tak interpretować?
Fizyka wahadło Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W istocie można to intepretować tak jak to zapisałaś - wtedy mamy do czynienia z innym przypadkiem, bo ruch nie zaczyna się już wtedy od maksymalnego wychylenia (amplitudy), ale od jakiegoś pośredniego. Wtedy potrzebowalibyśmy jeszcze informacji, w którą stronę w chwili początkowej przemieszcza się wahadło - czy w stronę położenia równowagi (wtedy ten czas będzie odpowiednio krótszy), czy w stronę maksymalnego wychylenia (wtedy będzie on oczywiście dłuższy). Samo obliczenie czasu stałoby się również wówczas bardziej kłopotliwe, wg mnie najprościej byłoby wtedy to zrobić wykorzystując wzór na zależnośc wychylenia z położenia równowagi x od czasu, czyli x(t) = A*sin*(wt) i na jego podstawie można byłoby obliczyć ile czasu zajmuje przejście np. z położenia równowagi do tego określonego wychylenia x (czyli wstawiamy omegę, A oraz x do tego wzoru i liczymy t), a stąd (znając ponadto okres drgań) doszlibyśmy do tego ile trwałoby przejście od tego wychylenia x do położenia równowagi (to zależy jeszcze jak już wcześniej wspomniałem, w którą stronę w chwili poczatkowej odbywałby się ruch). Więc można byłoby to tak interpretować, natomiast musiałyby tu zostać podana ta dodatkowa informacja, o której wspomniałem, no i wtedy na pewno nie byłoby to zadnanko do szybkiego zaznaczenia odpowiedzi za 1 pkt :)