Marcin 318 wyśw.
21-09-2024 14:56
2023C.1.2
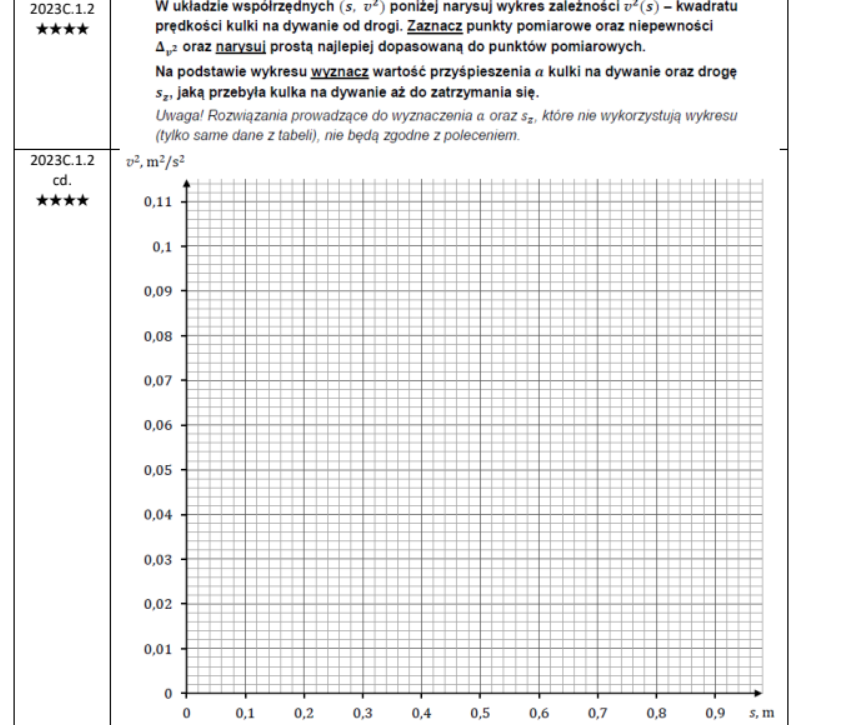
Jak wyznaczyć "a" z wykresu?
fizyka Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
s.gugula
21-09-2024 19:43
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zauważmy, że zgodnie z treścią zadania i tym co było celem w podpunkcie pierwszym, zależność kwadratu prędkości kulki od przebytej drogi jest następująca: v^2 = v0^2 - 2as. Ponieważ v0 (prędkość początkowa) oraz a (przyspieszenie, które mamy wyznaczyć) mają stałe wartości, to zależność v^2 od s jest zależnością liniową! A zatem punkty pomiarowe, które naniesiemy na wykres powinny układać się w linię prostą (będzie to funkcja malejąca), a współczynnikiem kierunkowym zgodnie z definicją funkcji liniowej będzie wyrażenie, które stoi przy zmiennej na osi poziomej (czyli przy s) - w naszym przypadku współczynnikiem kierunkowym jest zatem -2a. Jeśli zatem na podstawie wykresu wyznaczymy współczynnik kierunkowy prostej (to można zrobić biorąc np. dwa punkty z naszego wykresu i odczytując dla nich v^2 i s- w razie problemów z tą częścią obliczenia proszę śmiało pytać), to wystarczy go podzielić przez -2 i dostajemy szukane przyspieszenie a.