ZZ.3.1, ZZ.3.2./60
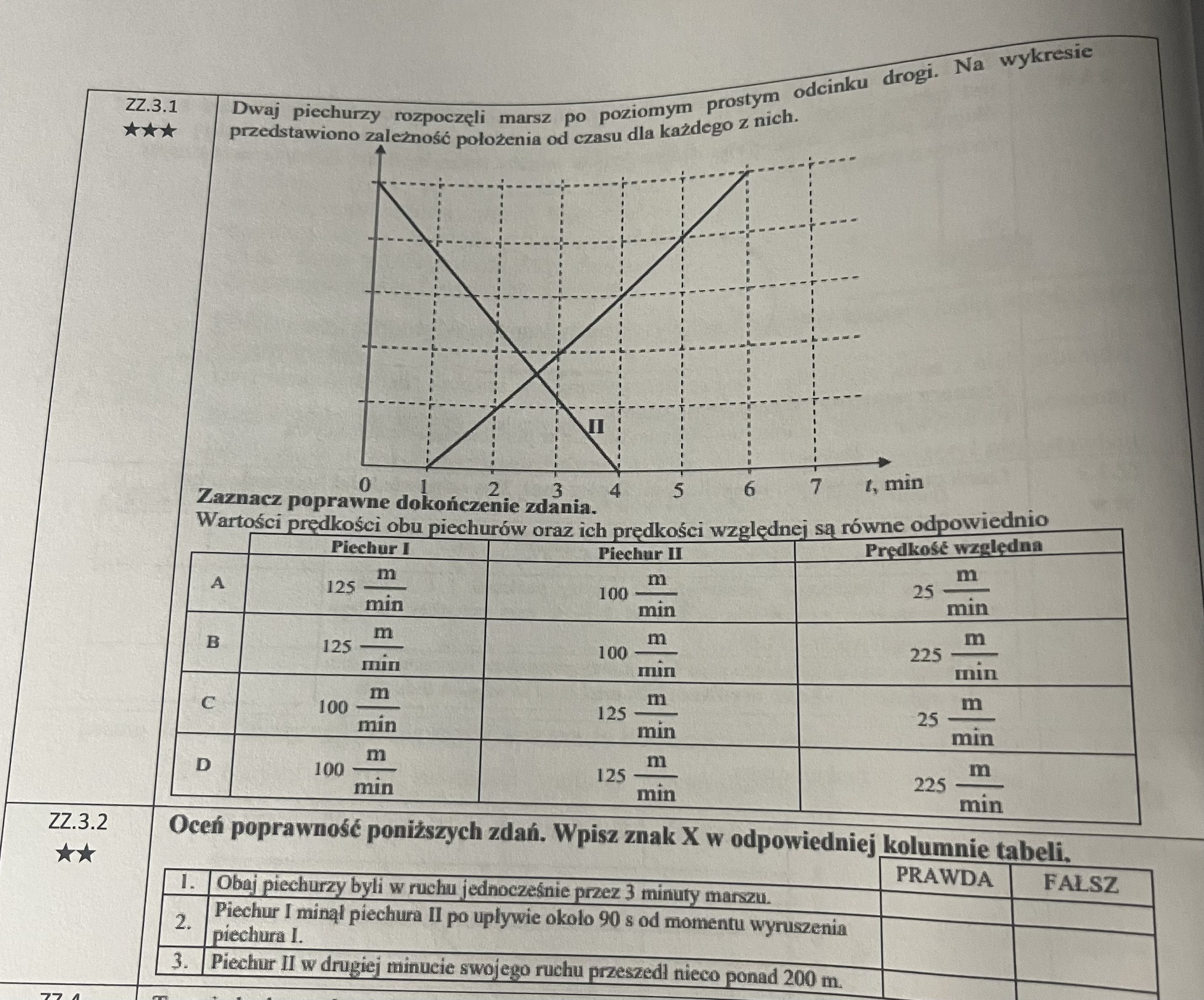
1) Skąd w ogóle wnioskować jakiekolwiek informacje do pdp. 3.1.? Nie ma wyskalowanej osi pionowej położenia. Nie wiem jak się do tego zabrać.
2) Jak odpowiedzieć na pytania 2 i 3 w pdp. 3.2. i dlaczego?
kurs z fizyki Dodaj post do ulubionych Poproś o pomoc
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1) W istocie nie ma wyskalowanej tu osi położenia i zapewne gdyby było to zadanie maturalne to wartości liczbowe normalnie by się tam pojawiły, ale tak się składa, że aby zrobić podpunkt pierwszy to nie są one nam potrzebne. Z charakterów obu wykresów możemy bowiem wywnioskować, który z piechurów poruszał się z większą prędkością, a na podstawie tego, że poruszali się oni w przeciwne strony (jeden wykres jest funkcją rosnącą, a drugi malejącą) możemy stwierdzić, że ich prędkość względna będzie sumą ich wartości prędkości. Stąd wywnioskujemy, która odpowiedź jest prawidłowa, nawet nie znając zawczasu skali na osi pionowej.
2) Zdanie 2: moment mijania się piechurów to moment, w którym ich położenia są takie same. Jest to zatem na wykresie punkt, w którym przecinają się obie proste. Możemy odczytać dla tego punktu czas i na tej podstawie stwierdzić czy to zdanie jest prawdziwe.
Zdanie 3: Druga minuta to przedział czasu od momentu t = 1 min do momentu t = 2 min. Trzeba zatem odczytać dla tych dwóch momentów położenie piechura nr 2, odjąć je od siebie i zobaczyć czy w istocie jest to "nieco ponad 200 m". Oczywiście, aby to stwierdzić potrzebna będzie nam już znajomość skali na osi pionowej, a tę możemy wywnioskować (a raczej obliczyć) już na podstawie odpowiedzi jaką uzyskamy w pp 1) (wyjdzie, że 1 kratka w pionie to 100 m).