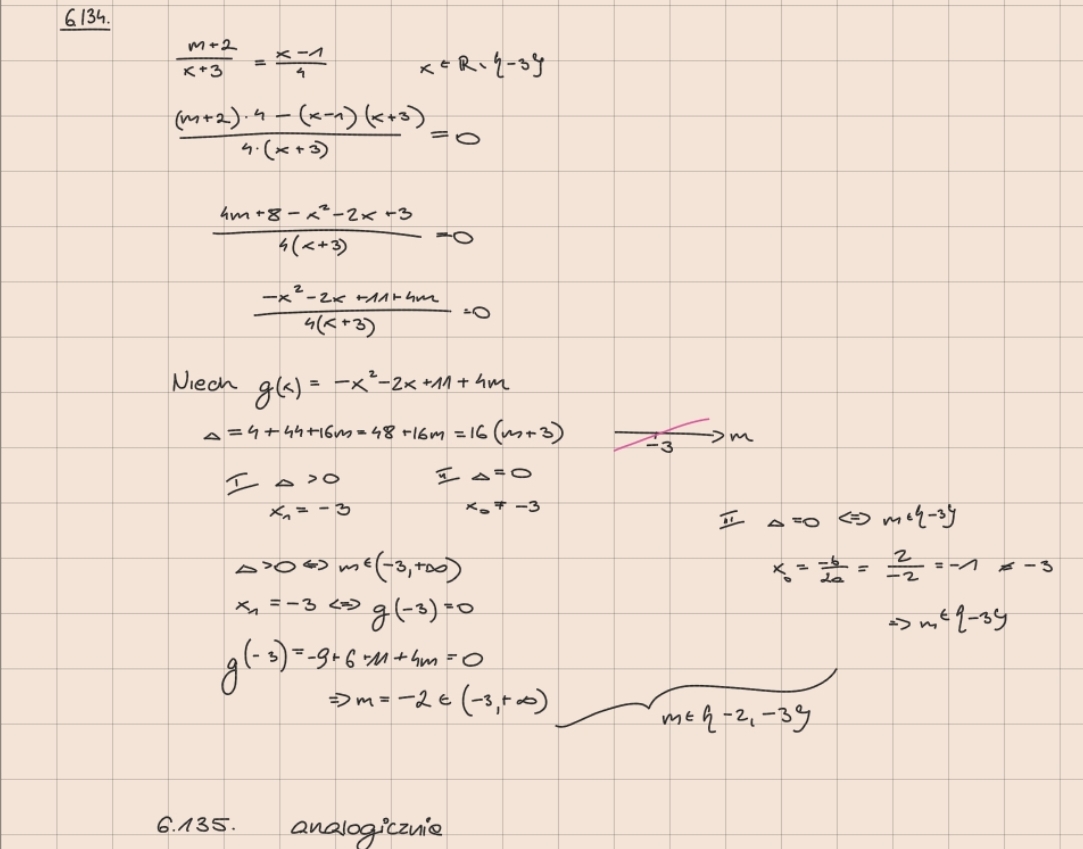Kurczab 6.134, 6.135
Jak doprowadzić te rozwiązania do dobrej odpowiedzi? Póki co dochodzę do sprzeczności z odpowiedzią :/
Matematyka Kurczab Dodaj post do ulubionych Poproś o pomoc
A dlaczego w 1 przypadku można przyjąć, że x=-3? Przecież to jest sprzeczność.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ponieważ, czysto teoretycznie dziedzina g(x) to wszystkie liczby rzeczywiste i dopiero po otrzymaniu miejsc zerowych wybieram takie, które mnie interesują (tu: inne od -3)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Mimo to jakoś dalej nie mogę tego zrozumieć :/
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Artur
Musimy spojrzeć na to zadanie w trochę inny sposób.
Przejdźmy do tego momentu po przekształceniach:
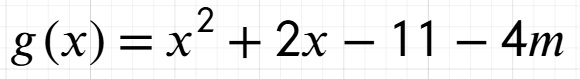
Założenie zostaje takie jak na początku tzn. x != 3
Szukamy takich m dla których ta funkcja ma jedno rozwiązanie.
Musimy się zatem zastanowić kiedy ta funkcja będzie miała jedno i tylko jedno rozwiązanie.
1) Funkcja ma dwa rozwiązania i jedno z nich jest równe 3. Wtedy musimy je odrzucić i zostaje tylko jedno poprawne (warunek spełniony).
2) Funkcja ma jedno rozwiązanie i jest ono różne od 3.
Czy to jest jasne ? Jeżeli nie to proszę śmiało pisać! :)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
I wtedy robimy sumę warunków zamiast części wspólnej?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, są to dwie niezależne sytuacje.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych