Zadanie domowe cz5, zadanie 4, str 90
Zad 4
Reszta z dzielenia wielomianu W(x) przez wielomian P(x) = x^3 +2x^2 -x -2
jest równa x^2+x+1. Wyznacz reszte z dzielenia wielomianu W(x) przez wielomian Q(x)= x^2 -1. (4 pkt)
Jeśli dobrze rozumiem to w zadaniu musimy wyzerować (x^3 +2x^2 -x -2)Q1(x), aby zostało nam W(x) = r i liczbami, które wyzerują to działanie będą miejsca zerowe tej funkcji P(x)= x^3 +2x^2 -x -2 czyli -2, 1, -1. Czy układu równań nie powinno się wiec zrobić z tych 3 miejsc zerowych następnie podstawionych do reszty? W(1)= 3, W(-1)=1 i W(-2)=3?
zadanie wielomiany praca domowa odpowiedzi Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Justyna, napewno miejsca zerowe Q(x)? Przecież w tym miejscu chyba nie jesteśmy w stanie ich określić?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Miejsca zerowe Q(x) = x^2 - 1 to 1 i -1, a muszę sprawdzić przynajmniej dwa (bo mam dwie niewiadome a i b), i takie, które się pokrywają z P(x)
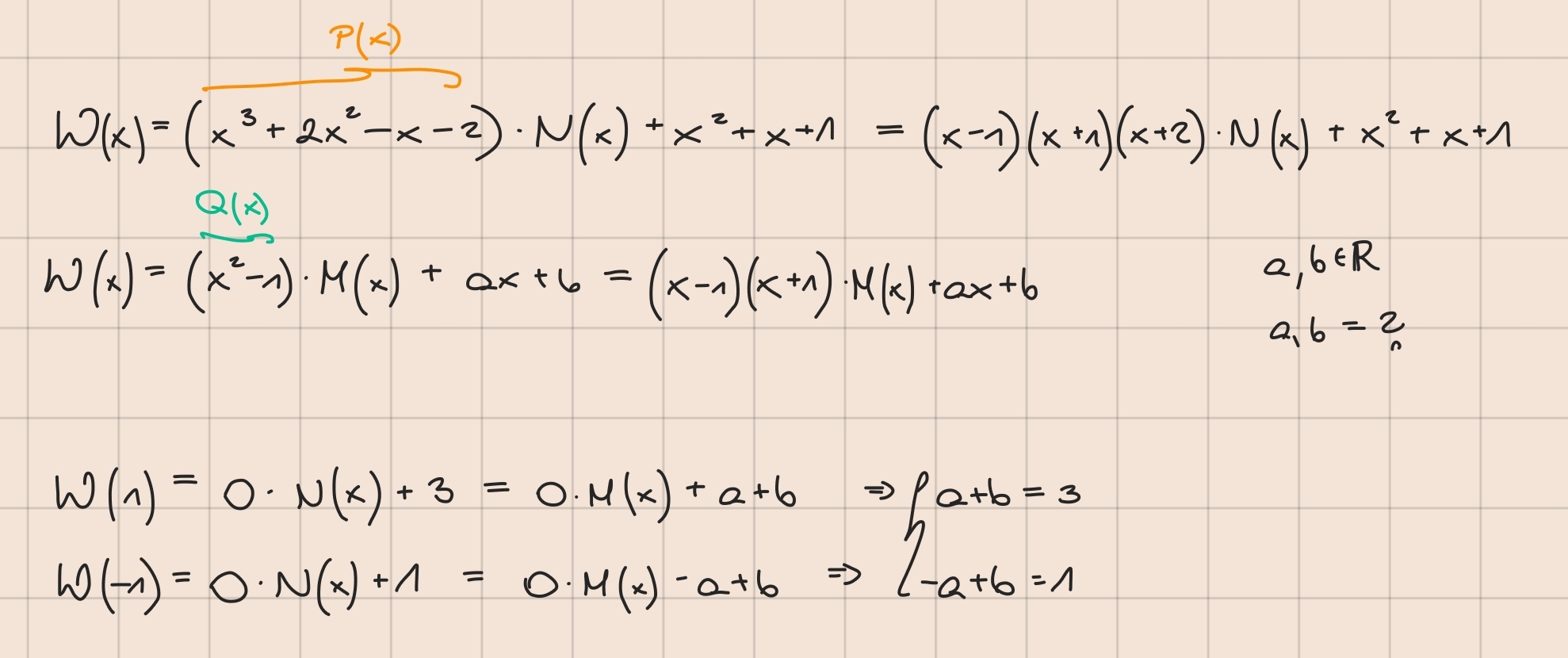
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Resztę z dzielenia Wielomianu przez dwumian (x-a) możemy określić zawsze, dla dowolnego a (mówi o tym tw. o reszcie W(a) = r). Jednak reszta ta nie zawsze będzie że tak powiem "ładna". Na przykład gdybyśmy chcieli poznać resztę z dzielenia wielomianu W(x) przez dwumian (x-3) to zgodnie z tw. o reszcie podstawilibyśmy do W(x) 3 i dla W(x) = (x³ + 2x² - x - 2) * S(x) + x² + x + 1 otrzymalibyśmy resztę W(3) = 40 * S(3) + 13. Jako, że nie znamy wzoru wyniku tego dzielenia czyli S(x) to nic nam ta reszta nie mówi. Właśnie dlatego P(x) rozkładamy na postać iloczynową (x+2)(x-1)(x+1). Dzięki przedstawieniu W(x) w takiej formie W(x) = (x+2)(x-1)(x+1) * S(x) + x² + x + 1 jesteśmy w stanie określić "ładną" resztę z dzielenia tego wielomianu w 3 konkretnych przypadkach (a dokładnie resztę z dzielenia W(x) przez (x+2), resztę z dzielenia W(x) przez (x-1) i resztę z dzielenia W(x) przez (x+1). A jesteśmy w stanie to zrobić, ponieważ chcąc poznać resztę z dzielenia wielomianu W(x) przez jeden z tych dwumianów liniowych to zgodnie z tw. o reszcie podstawiamy wyraz wolny tego dwumianu i voila jeden z nawiasów nam się zeruje, pozbywamy się nieznanego nam S(x), a to co nam zostaje to "ładna" reszta.
W(-2) = (-2+2)(-2-1)(-2+1) * S(x) + 4 -2 + 1 = 0 * (-3) * (-1) * S(x) + 3 = 3 = W(-2)
W(1) = (1+2)(1-1)(1+1) * S(x) + 1 + 1 + 1 = 3 * 0 * 2 * S(x) + 3 = 3 = W(1)
W(-1) = (-1+2)(-1-1)(-1+1) * S(x) + 1 -1 + 1 = 1 * (-2) * 0 * S(x) + 1 = 1 = W(-1)
Teraz mamy znaleźć resztę z dzielenia wielomianu W(x) przez Q(x). Rozkładamy Q(x) = (x² - 1) na (x-1)(x+1) i jednocześnie wiemy, że stopień reszty musi być mniejszy od stopnia dzielnika Q(x) czyli w tym przypadku reszta ma stopień co najwyżej 1, a więc jej wzór ogólny możemy zapisać w postaci R(x) = ax + b czyli mamy W(x) = (x-1)(x+1) * S₂(x) + ax + b. Teraz musimy znaleźć a i b i od razu widzimy, że w tym przypadku możemy uzyskać 2 "ładne" reszty, bo dla dwóch wartości x możemy się pozbyć S₂(x). tak robimy.
W(1) = (1-1)(1+1) * S₂(x) + a + b = 0 * 2 * S₂(x) + a + b = a + b = W(-1)
W(-1) = (-1-1)(-1+1) * S₂(x) -a + b = (-2) * 0 * S₂(x) - a + b = -a + b = W(-1)
Teraz przypominamy sobie, że znamy W(1) i W(-1) (czyli reszty z dzielenia tego wielomianu przed dwumiany (x-1) i (x+1)). Zostało, więc już tylko podstawić pod W(1) i W(-1) poznane wcześniej wartości i rozwiązać prosty układ 2 równań z dwoma niewiadomymi.
Przepraszam, że tak się rozpisałem. Jak coś mnie zainteresuje to zaczynam to rozkładać na czynniki pierwsze i pomyślałem, że przy okazji podzielę się swoimi przemyśleniami, a nóż widelec komuś coś to rozjaśni ;D Pozdrawiam
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wydaje mi się, że należy sprawdzić nie tyle miejsca zerowe P(x), o ile miejsca zerowe Q(x) - wtedy jest ich tylko dwa oraz, celowo lub nie, pokrywają się one częściowo z pierwiastkami P(x)