2012C.1.3 strona 47

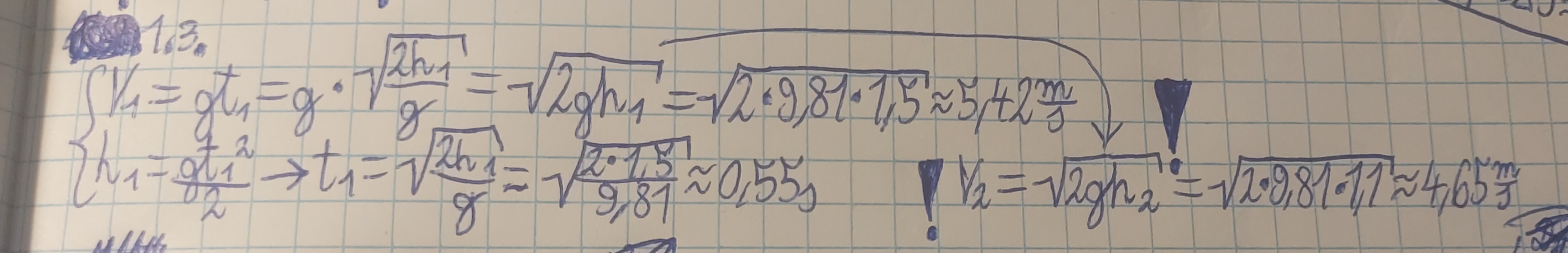
Dlaczego V2 obliczamy z tego samego wzoru co V1 tylko podstawiając h2 zamiast h1? (spisałem to z odpowiedzi cke)
Fizyka dynamika Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A no tak, próbowałem zrobić w ten sposób i mi nie wyszło, bo myślałem że Vkprzed upadkiem =V0 po upadku a przecież są opory ruchu.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W kwestii straty energii nie chodzi nawet o opory ruchu co raczej przeznaczenie części tej energii na ciepło kulki (co w treści jest nawet zapisane, że część energii poszła na zwiększenie energii wewnętrznej kulki). Tak czy siak są tutaj w momencie odbicia straty energii kinetycznej.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Mogłyby się pojawić inne formy "utraty" energii - np. część energii mogłaby przejść w energię potrzebną do odkształcenia kulki w momencie odbicia. Gdyby jednak nie było żadnego takiego zjawiska, to tak - w momencie odbicia nie mielibyśmy strat energii - natomiast z uwagi na istnienie oporu powietrza straty energii i tak pojawiłyby się podczas wznoszenia kulki, więc wysokość, na którą się ona wzniesie i tak byłaby mniejsza od tej, z której pierwotnie została upuszczona.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale gdyby działały tylko opory ruchu, to nie zmniejszyłyby one prędkości piłki tuż po odbiciu?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ruch w górę jest teraz ruchem jednostajnie opóźnionym, więc dla niego możemy zapisać analogiczne równania kinematyczne na prędkość i drogę, czyli vk = v0 - gt (v0 to to co chcemy policzyć) oraz s = v0*t - gt^2/2. Ponieważ końcowa prędkość jest zerowa, to vk = 0. Z tego układu równań możemy wyznaczyć teraz zależność między v0 i s - okazuje się, że dojdziemy do dokładnie takiej samej postaci jak w przypadku prędkości końcowej w ruchu jednostajnie przyspieszonym (obliczone wcześniej v1), czyli: v0 = pierw(2*g*s), co w przypadku tego zadania oznacza, że v2 = pierw(2*g*h2).