Kubix 120 wyśw. 27-10-2024 20:13

Zad.1 przykład j - zadanie domowe 3 cz.1


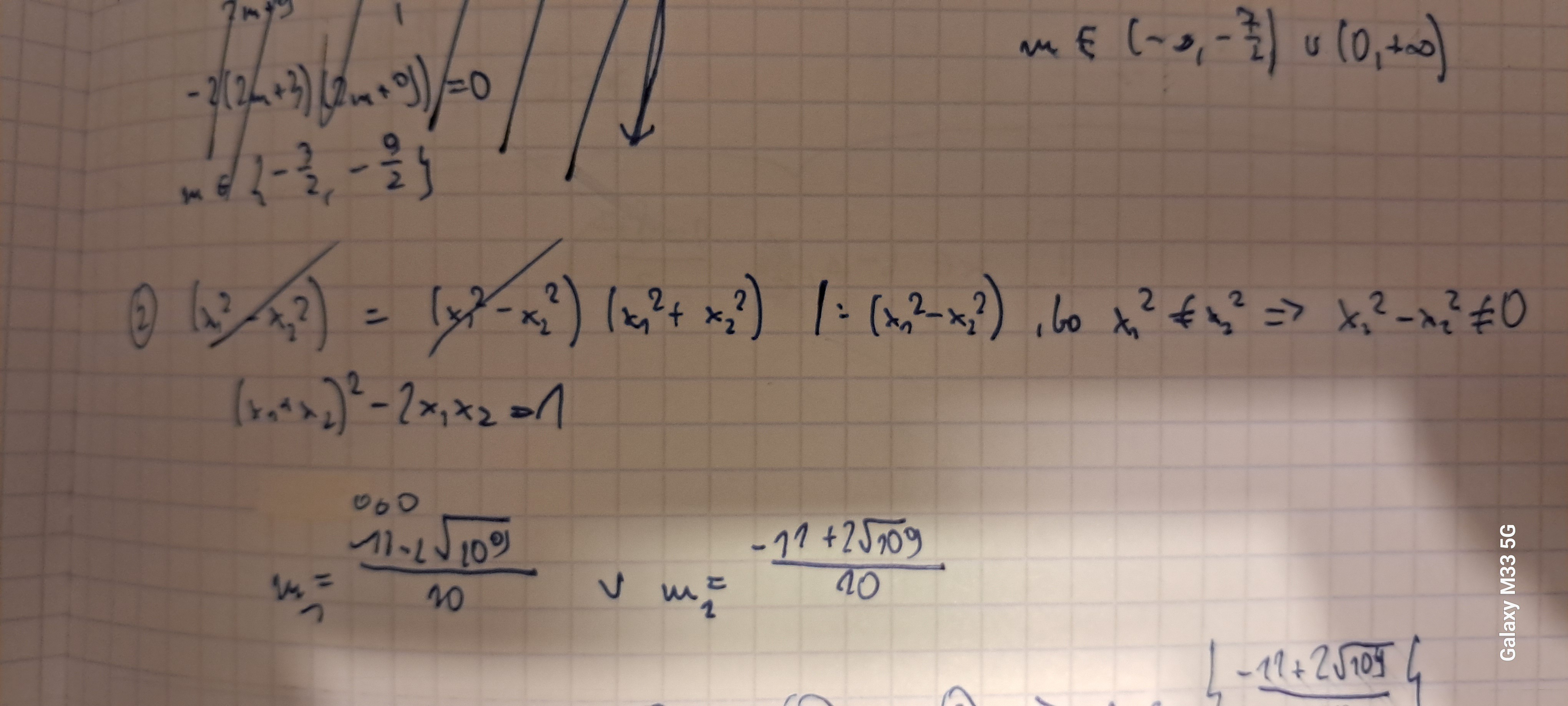
Cześć, zadanie 13 robiliśmy na lekcji i było powiedziane ze nie mozna skracać wyrażenie x1^2-x2^2 tylko trzeba przenieść na drugą stronę. Identyczne zadanie było w pracy domowej i tam można skrócić z odpowiednim uzasadnieniem. Jaka wersja jest poprawna, bo jedno wyklucza drugie i się pogubiłem?
Matematyka Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Kuba 28-10-2024 15:51

Nie możesz skracać gdy wyrażenie może być zerem. W zadaniu domowym miejsca zerowe muszą być różne od siebie więc x1-x2 nigdy nie będzie zerem. Odejmujesz od jakiejś liczby inną liczbę więc jest to niemożliwe aby z takiego wyrażenia wyszło zero

Kubix 28-10-2024 18:31

Dzięki, ale właśnie polecenia są identyczne i pisze, że mają być różne miejsca zerowe w obu zadaniach, dlatego nadal nie rozumiem dlaczego na lekcji przenieśliśmy wyrażenie na drugą stronę, skoro wiadomo, że nie będzie równe zero?

jarosinski 31-10-2024 23:04
Wszystko jest prawidłowe: nie można tego wyrażenia skrócić w zadaniu na lekcji ponieważ x1+x2 może się wyzerować. A w zadaniu domowym można skrócić ponieważ to wyrażenie nie może się wyzerować (ale trzeba to uzasadnić). Także wszystko gra :)