Anna.N 33 wyśw. 28-10-2024 20:47

Zadanie domowe 6, zad. 3.1, część II


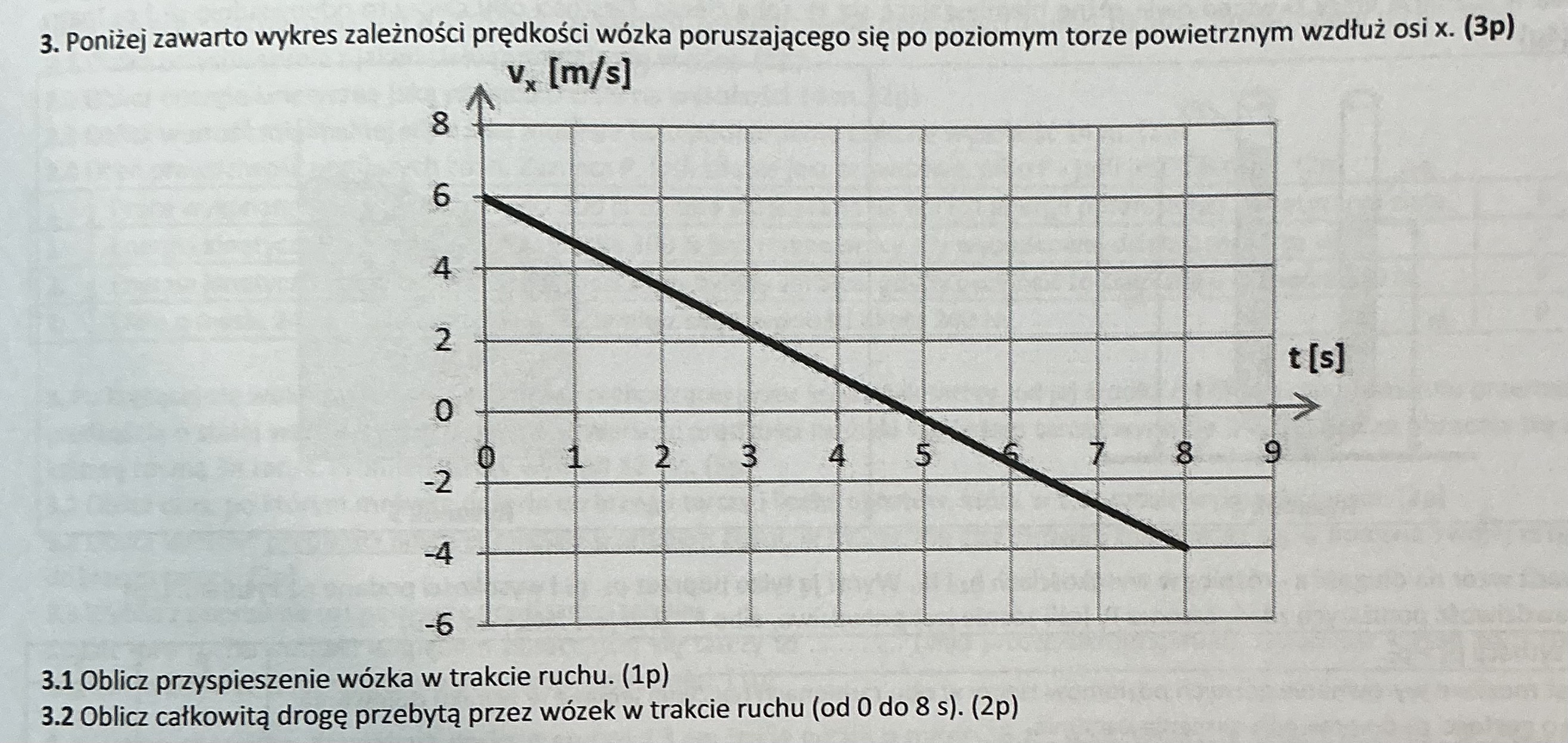
Dlaczego takie rozwiązanie jest błędne, skoro mamy wykres współrzędnej x prędkości od czasu, więc kiedy wartość jest dodatnia - ruch wózka odbywa się zgodnie ze zwrotem osi x, a gdy wartość jest ujemna - przeciwnie to zwrotu osi x.

Tak więc same wartości prędkości zawsze są dodatnie (ujemna wartość na wykresie świadczy tylko o zwrocie). Zatem w t=0s v=6m/s, natomiast w t=8s v=4m/s. Wyliczając wartość przyspieszenia ze wzoru, przy liczeniu delta v wzięłam wartość bezwzględną, aby po prostu wyznaczyć wartość przyspieszenia. 

Dlaczego taki rozwiązanie jest złe?

Fizyka Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
s.gugula 29-10-2024 12:13

Takie wyliczenie byłoby prawdziwe, gdyby prędkość tutaj zmieniała się od wartości 6 m/s poprzez 5,5 m/s, następnie 5 m/s itd. aż do 4 m/s. natomiast tutaj tak nie jest, właśnie z uwagi na fakt, że zmienia się zwrot prędkości. Czyli zmiana tutaj wygląda następująco: 6 m/s -> 5 m/s -> 4 m/s -> 3 m/s -> ... -> 0 m/s -> - 1 m/s -> ... -> - 4 m/s (minus oczywiście świadczy o przeciwnym zwrocie). A zatem zmiana wektora prędkości jest dużo większa niż w zaproponowanym przez Ciebie obliczeniu.

Można to wytłumaczyć również bardziej formalnie wykorzystując definicję przyspieszenia. Przyspieszenie jest wektorem, więc w jego definicji występująca w liczniku zmiana prędkości również jest wektorem! Wartość takiego wektora nie jest zwyczajnie różnicą wartości końcowej i poczatkowej - trzeba by najpierw wyznaczyć (można to zrobić nawet geometrycznie na rysunku) wektor zmiany predkości i dopiero wtedy policzyć jego wartość. Okazuje się, że jest ona równa 10 m/s. Analogiczną rzecz robiliśmy na zajęciach gdy rozwiązywaliśmy zadanie z siła i zmianą pędu. Wartość wektora zmiany pędu (deltap) nie mogła być policzona jako różnica wartości końcowej i początkowej, tylko trzeba było najpierw wyznaczyć ten wektor (robiliśmy to tam graficznie na rysunku) i dopiero wtedy policzyć jego wartość (to było zad. INF. 1).