MarcinC 42 wyśw. 31-10-2024 20:43

Matura 2017.C.11

w przedziale <0, 2pi> rozwiąż

3sin(x-pi/4) + cos(x+pi/4)=1

Mam pytanie. Czy da się jakoś matematycznie wytłumaczyć na poziomie szkoły średniej dlaczego przy zastosowaniu sumy sinusów (oznaczenie gwiazdką) wychodzi sprzeczność a przy wykorzystaniu nieparzystości funkcji sinus wychodzi łatwo i szybko. Ja przyznam, ze nie dostrzegłem tego szybkiego sposobu i zrobiłem drugim znacznie dłuższym. Tam gdzieś pojawia się dzielenie przez zero przy złym rozwiązaniu oznaczonym gwiazdką?

Tak jak teraz myślę, to funkcje są łącznie przesunięte o pi/2 a cosinus dla pi/2 ma wartość zero i to może powoduje dzielenie przez zero i sprzeczność?



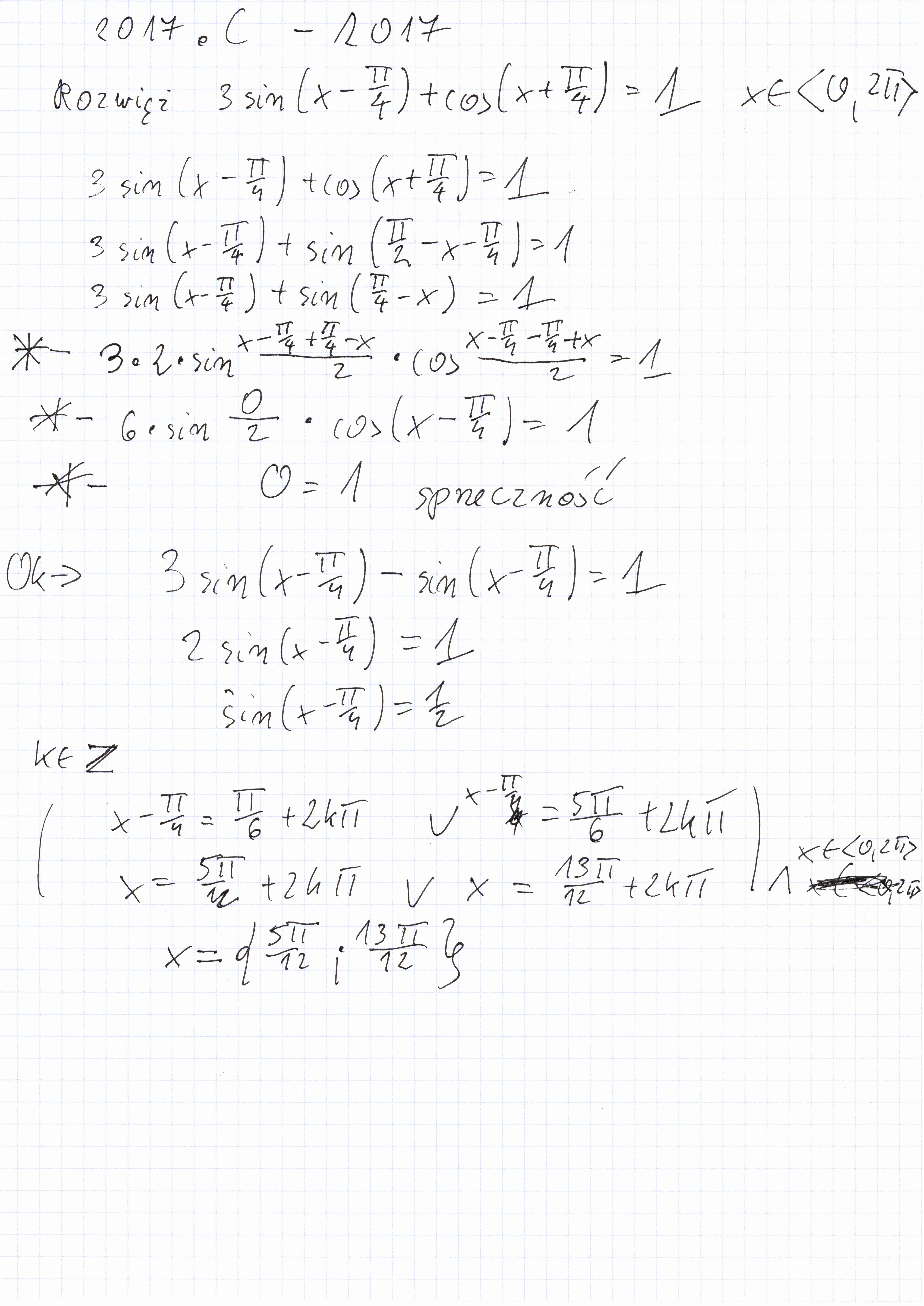
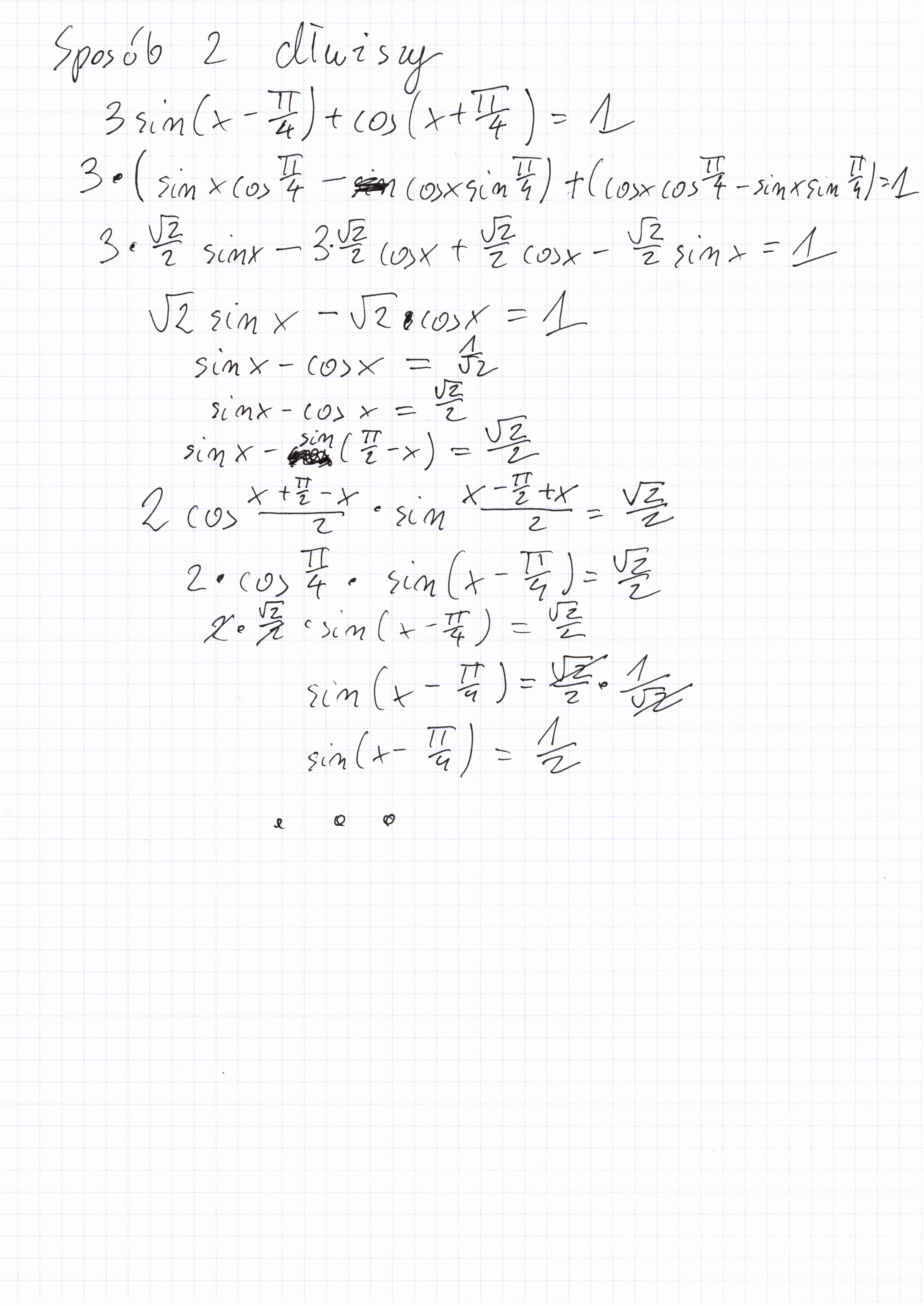
Trygonometria Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 01-11-2024 23:04

Błędnie zastosowałeś wzór na sumę sinusów, rozbij sobie 3sin(x-pi/4) na sin(x-pi/4)+sin(x-pi/4)+sin(x-pi/4) + sin(pi/4-x)=1