martasiema 31 wyśw. 11-11-2024 04:32

2021.12


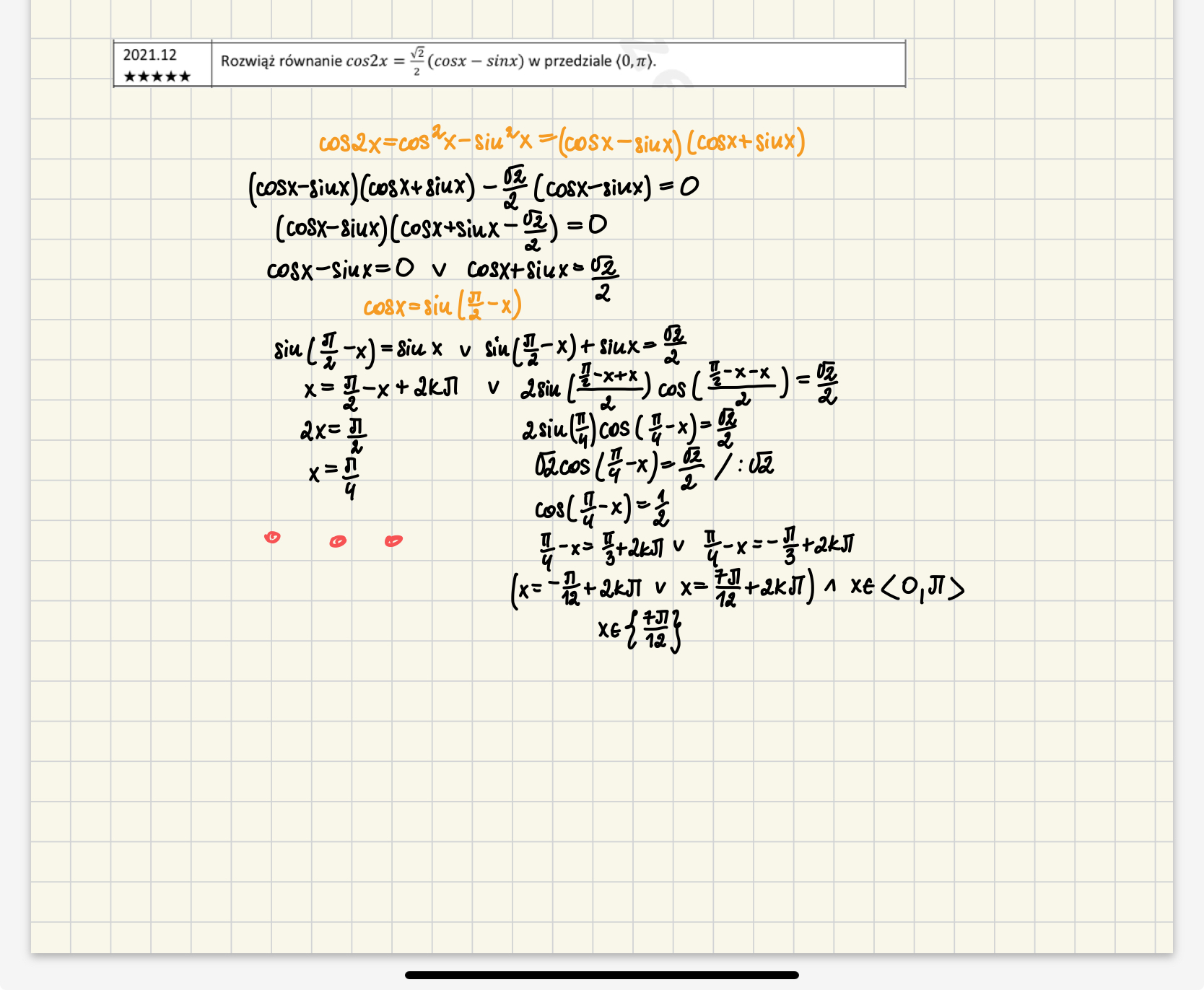
jak dokończyć tą część, gdzie są 3 kropki?

trygonometria Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Antoni Buks 11-11-2024 11:40

Przy przekształceniach znikło wyrażenie: +2kπ

Końcowo powinno wyjść: x=π/4 + kπ

Co daje nam rozwiązanie: π/4

martasiema 11-11-2024 18:19

aa bo to 2kpi dopisałam patrząc na przykładowe odpowiedzi. ale właśnie nie wiem czemu to trzeba dopisać

edit. 1. szukając jak rozwiązać cosx=sinx znalazłam taki sposób, że sinx/cosx=1 tgx=1 x=pi/4 + kpi, czy to jest poprawne? bo przecież nie można dzielić przez zmienne

2. jeśli użyjemy innego wzoru redukcyjnego to cosx=sin(pi/2+x) i wtedy pi/2=0 więc tym bardziej nie wiem jak rozwiązać sinx=cosx