2012.5.1 strona 95
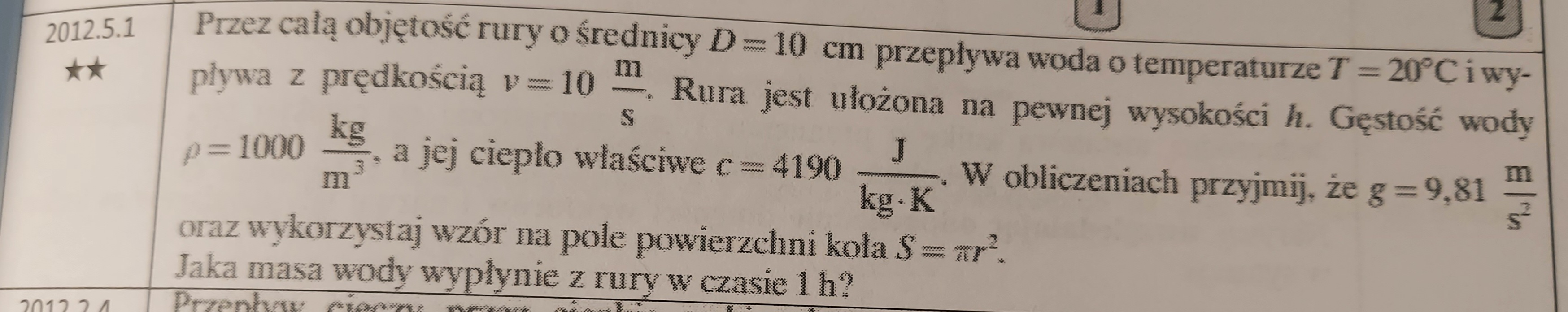

Jak podejść do tego zadania?
Bo chyba ani siły, ani ZZE nie prowadzą do rozwiązania.
Fizyka hydrostatyka Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale jeśli tutaj d=V(prędkość)*t i przyjmujemy, że rura leży poziomo to V=10m/s=const., więc to znaczyłoby, że im dłużej woda płynie(więcej czasu) tym przez dłuższą część rury przepływa. Czy to nie doprowadziłoby do tego, że dla pewnego czasu "rura się wydłuży"?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
To raczej należałoby interpretować tak, że dla dłuższego czasu t, z rury zdąży wypłynąc większa ilość wody, czyli taka, że objętość tej wody jest równa S*d, które to d jest teraz po prostu większe.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dobrze, czyli w takim razie przekombinowałem chyba. Dziękuję :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ono jest prostsze niż się wydaje ;) nie ma tu w ogóle potrzeby wchodzenia w siły, ani ZZE, najwygodniej jest w ogóle przyjąć sobie, że rura leży w poziomie. Wtedy możemy zauważyć, że w czasie t z rury wypływa pewna objętość V wody, którą możemy zapisać poprzez pole jej przekroju S oraz poprzez prędkość wypływu wody v. Używając następnie zależności między masą, gęstością i objętością, łatwo obliczymy masę wypływającej wody. Zamieściłem to pobieżnie na rysunku poniżej.