Zadanie o czworokącie

1-Prawda (te trójkąty mają wysokości o tej samej długości opuszczone na podstawę, więc AB=3CD)

2-Prawda (wysokością tych trójkątów jest wysokość trapezu-odległość między podstawami AB i CD)

3-Fałsz (kąt mógłby być prosty, ale nie ostry, bo wtedy nie będzie to trapez)

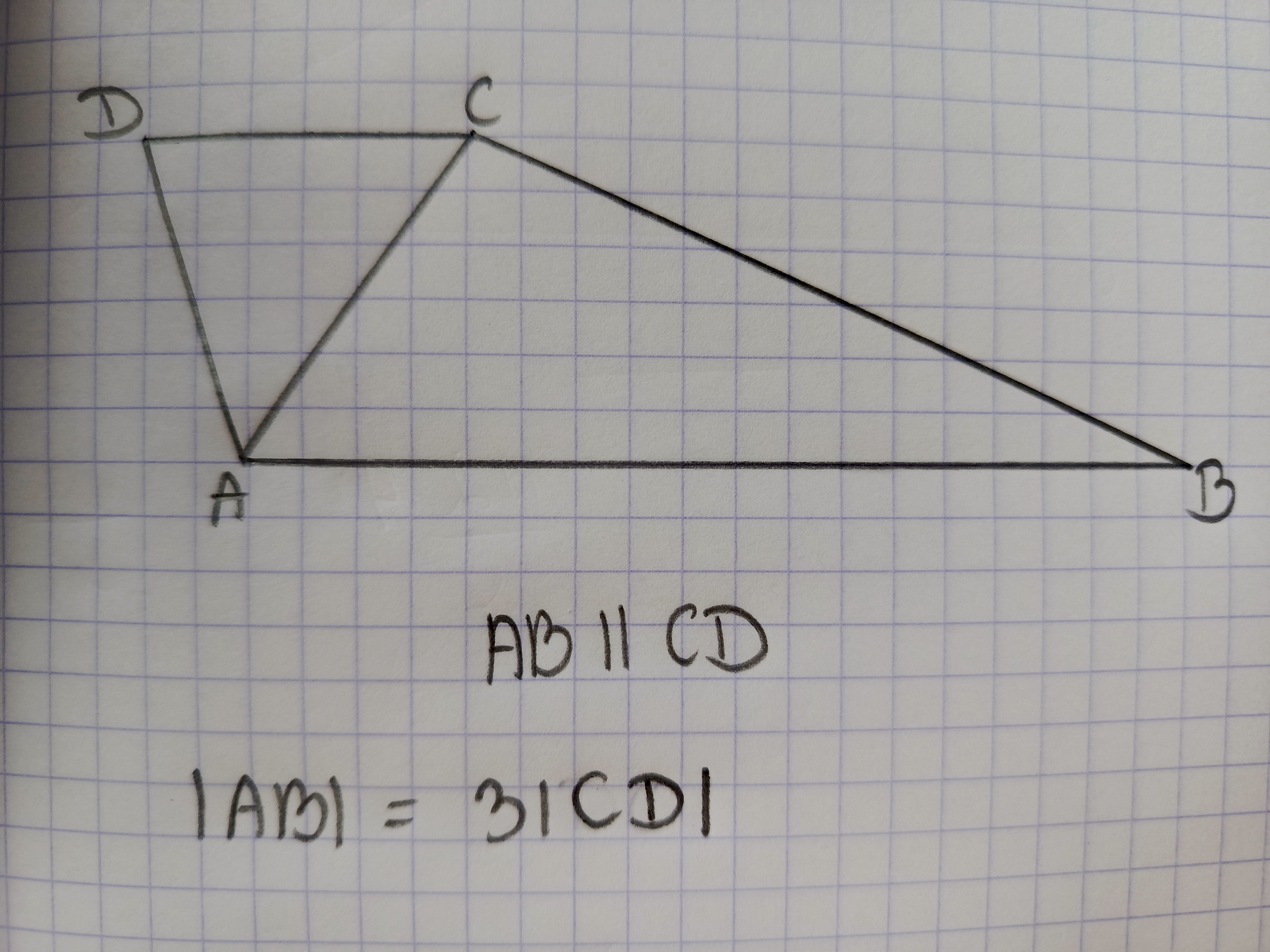
Mam pytanie dotyczące tego 3 podpunktu. Dlaczego gdyby trójkąt ADC był ostrokątny to ABCD nie byłby trapezem (podstawy ABCD dalej byłyby przecież równoległe)?

No bo z podpunktu 1 wyszło, że AB=3CD, więc CD jest krótsze, a przy krótszej podstawie kąty w trapezie są rozwarte (albo w granicznym przypadku jeden z tych kątów jest prosty). Gdyby trójkąt ADC był ostrokątny to czworokąt ABCD byłby np. równoległobokiem.

Tak, i skoro byłby równoległobokiem, to i trapezem, bo ma przynajmniej jedną parę boków równoległych. Jednak w tym przypadku wydaje mi się, że nie byłby to równoległobok - ramiona trapezu nie byłyby równoległe (bo i podstawy nie byłyby takiej samej długości z punktu 1). Ale właśnie nie jestem pewna czy nie byłby to trapez różnoramienny (AB || CD).

No ale w zadaniu masz dane, że ABCD to trapez i owszem równoległobok jest trapezem, ale trapez nie jest równoległobokiem.

No tak, ale dlaczego nie mógłby być to trapez różnoramienny (taki jak wcześniej dodałam na zdjęciu)?

Skoro da się podać przykład takiego trapezu to znaczy, że on istnieje i może być ostrokątny