majamitura 33 wyśw.
16-11-2024 20:33
matura 2015 zadanie 9
Dany jest sześcian ABCDEF GH o krawędzi długości 2. Punkt P jest środkiem krawędzi BC .
Płaszczyzna AHP przecina krawędź CG w punkcie R (zobacz rysunek). Oblicz pole przekroju tego
sześcianu płaszczyzną przechodzącą przez punkty A ,H ,R i P .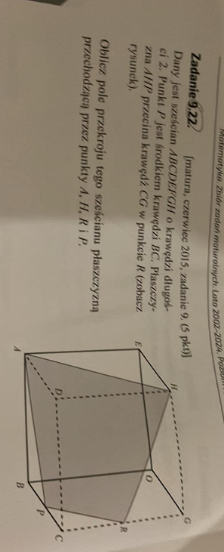
Bardzo proszę o uzasadnienie dlaczego krawędz CG zostala akurat podzielona na odcinki 1 i 1 że ten przekrój jest trapezem równoramiennym. Coś więcej niż że AH jest rownoległe do PR. Nie mogę sobie tego wyobrazić bardzo proszę o uzasadnienie z góry dziękuje:)
matura rozszerzona Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski
20-11-2024 11:02
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Rzeczywiście może to być kłopotliwe do wyobrażenia sobie za pierwszym razem, ale kluczem jest to, że AH jest równoległe do PR. Dodatkowo zwróć uwagę na to, że płaszczyzna przechodząca przez punkt P oraz H jest symetryczna względem sześcianu.
Z tego, że punkt R dzieli CG na równe części już wynika równoramienność trapezu gdyż trójkąty:
ABP i HGR są przystające (wszystkie boki równej długości).